排列组合常用方法总结(全)
解决排列组合问题常见策略
学习指导
1、排列组合的本质区别在于对所取出的元素是作有序排列还是无序排列。组合问题可理解为把元素取出后放到某一集合中去,集合中的元素是无序的。
较复杂的排列组合问题一般是先分组,再排列。必须完成所有的分组再排列,不能边分组边排列。
排列组合问题的常见错误是重复和遗漏。弄清问题的实质,适当的分类,合理的分步是解决这个错误的关键,采用不同的思路检验结果是否一致是解决这个错误的技巧。
集合是常用的工具之一。为了将抽象问题具体化,可以从特殊情形着手,通过画格子,画树图等帮助理解。
“正难则反”是处理问题常用的策略。
常用方法:
一. 合理选择主元
例1. 公共汽车上有3个座位,现在上来5名乘客,每人坐1个座位,有几种不同的坐法?
例2. 公共汽车上有5个座位,现在上来3名乘客,每人坐1个座位,有几种不同的坐法?
分析:例1中将5名乘客看作5个元素,3个空位看作3个位置,则问题变为从5个不同的元素中任选3个元素放在3个位置上,共有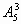 种不同坐法。例2中再把乘客看作元素问题就变得比较复杂,将5个空位看作元素,而将乘客看作位置,则例2变成了例1,所以在解决排列组合问题时,合理选择主元,就是选择合适解题方法的突破口。
种不同坐法。例2中再把乘客看作元素问题就变得比较复杂,将5个空位看作元素,而将乘客看作位置,则例2变成了例1,所以在解决排列组合问题时,合理选择主元,就是选择合适解题方法的突破口。
二. “至少”型组合问题用隔板法
对于“至少”型组合问题,先转化为“至少一个”型组合问题,再用n个隔板插在元素的空隙(不包括首尾)中,将元素分成n+1份。
例5. 4名学生分6本相同的书,每人至少1本,有多少种不同分法?
解:将6本书分成4份,先把书排成一排,插入3个隔板,6本书中间有5个空隙,则分法有:
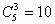 (种)
(种)
三. 注意合理分类
元素(或位置)的“地位”不相同时,不可直接用排列组合数公式,则要根据元素(或位置)的特殊性进行合理分类,求出各类排列组合数。再用分类计数原理求出总数。
例6. 求用0,1,2,3,4,5六个数字组成的比2015大的无重复数字的四位数的个数。
解:比2015大的四位数可分成以下三类:
第一类:3×××,4×××,5×××,共有: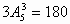 (个);
(个);
第二类:21××,23××,24××,25××,共有: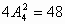 (个);
(个);
第三类:203×,204×,205×,共有: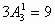 (个)
(个)
∴比2015大的四位数共有237个。
四. 特殊元素(位置)用优先法
把有限制条件的元素(位置)称为特殊元素(位置),对于这类问题一般采取特殊元素(位置)优先安排的方法。
例1. 6人站成一横排,其中甲不站左端也不站右端,有多少种不同站法?
分析:解有限制条件的元素(位置)这类问题常采取特殊元素(位置)优先安排的方法。
解法1:(元素分析法)因为甲不能站左右两端,故第一步先让甲排在左右两端之间的任一位置上,有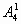 种站法;第二步再让其余的5人站在其他5个位置上,有
种站法;第二步再让其余的5人站在其他5个位置上,有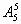 种站法,故站法共有:
种站法,故站法共有: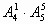 =480(种)
=480(种)
解法2:(位置分析法)因为左右两端不站甲,故第一步先从甲以外的5个人中任选两人站在左右两端,有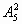 种;第二步再让剩余的4个人(含甲)站在中间4个位置,有
种;第二步再让剩余的4个人(含甲)站在中间4个位置,有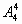 种,故站法共有:
种,故站法共有: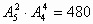 (种)
(种)
五. 分排问题用直排法
对于把几个元素分成若干排的排列问题,若没有其他特殊要求,可采取统一成一排的方法求解。
例5. 9个人坐成三排,第一排2人,第二排3人,第三排4人,则不同的坐法共有多少种?
解:9个人可以在三排中随意就坐,无其他限制条件,所以三排可以看作一排来处理,不同的坐标共有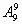 种。
种。
六. 复杂问题用排除法
对于某些比较复杂的或抽象的排列问题,可以采用转化思想,从问题的反面去考虑,先求出无限制条件的方法种数,然后去掉不符合条件的方法种数。在应用此法时要注意做到不重不漏。
例6. 四面体的顶点和各棱中点共有10个点,取其中4个不共面的点,则不同的取法共有( )
A. 150种 B. 147种 C. 144种 D. 141种
解:从10个点中任取4个点有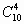 种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有
种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有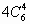 种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三类情况不合要求应减掉,所以不同的取法共有:
种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三类情况不合要求应减掉,所以不同的取法共有: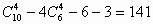 (种)。
(种)。
七. 多元问题用分类法
按题目条件,把符合条件的排列、组合问题分成互不重复的若干类,分别计算,最后计算总数。
例7. 已知直线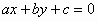 中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数。
中的a,b,c是取自集合{-3,-2,-1,0,1,2,3}中的3个不同的元素,并且该直线的倾斜角为锐角,求符合这些条件的直线的条数。
解:设倾斜角为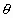 ,由
,由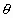 为锐角,得
为锐角,得 ,即a,b异号。
,即a,b异号。
(1)若c=0,a,b各有3种取法,排除2个重复(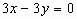 ,
,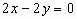 ,
,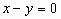 ),故有:3×3-2=7(条)。
),故有:3×3-2=7(条)。
(2)若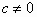 ,a有3种取法,b有3种取法,而同时c还有4种取法,且其中任意两条直线均不相同,故这样的直线有:3×3×4=36(条)。
,a有3种取法,b有3种取法,而同时c还有4种取法,且其中任意两条直线均不相同,故这样的直线有:3×3×4=36(条)。
从而符合要求的直线共有:7+36=43(条)
八. 排列、组合综合问题用先选后排的策略
处理排列、组合综合性问题一般是先选元素,后排列。
例8. 将4名教师分派到3所中学任教,每所中学至少1名教师,则不同的分派方案共有多少种?
解:可分两步进行:第一步先将4名教师分为三组(1,1,2),(2,1,1),(1,2,1),共有: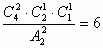 (种),第二步将这三组教师分派到3种中学任教有
(种),第二步将这三组教师分派到3种中学任教有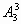 种方法。由分步计数原理得不同的分派方案共有:
种方法。由分步计数原理得不同的分派方案共有: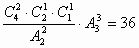 (种)。因此共有36种方案。
(种)。因此共有36种方案。
九.顺序问题用“除法”
对于几个元素顺序一定的排列问题,可先把这几个元素同其余元素一同进行排列,然后用总的排列数除以这几个元素的全排列数。
例:7个节目,甲、乙、丙三个节目按给定顺序出现,有多少种排法?
分析:7个节目的全排列为A77,甲、乙、丙之间的顺序已定。所以有A77∕A33=840种。
答案:840种。
十.特征分析
研究有约束条件的排数问题,需紧扣题中所提供的数字特征,结构特征,进行推理,分析求解。
例:由1,2,3,4,5,6这六个数可组成多少个无重复且是6的倍数的五位数?
分析:6的倍数既是2的倍数,又是3的倍数。是2的倍数,个位上为2、4或6;是3 的倍数必须满足各个数字上的数字之和是3的倍数的特征。把这6个数分组(3)、(6)、(1,5)、(2,4),每组的数字和都是3的倍数,因此可分成两类讨论。第一类:由1、2、4、5、6作数码,首先从2、4、6中任选一个作为个位数字,有A31种,然后其余4个数字在其它数字上全排列有A44,所以,N1=A31A44个,第二类:由1、2、3、4、5作数码,依上法有N2=A21A44个。故N=N1+N2=120个。
答案:120个。
十一、对应
有些时候,一个事件与一个结果之间存在一一对应的关系。
例:在100名选手之间进行单循环淘汰赛(即一场比赛后,失败者退出比赛),最后产生一名冠军,需举行多少场比赛?
分析:要产生一名冠军,需要淘汰99名选手。要淘汰掉一名选手,必须举行一场比赛;反之,每场比赛恰淘汰一名选手。两者之间一一对应。故要淘汰99名选手,应举行99场比赛,从而产生一名冠军。
十二、用比例法
有些排列应用题,可以根据每个元素出现机会占整个问题的比例,从而求得问题的结果。
例:从6个运动员中选出4个参加4×100 米接力赛。如果甲、乙都不能跑第一棒,那么共有多少种不同的参赛方案?
分析:若不受条件限制,则参赛方案有A64=360种,但其中限制甲、乙两人不能跑第一棒,即跑第一棒的只能是其他的人,而这4人在第一棒中出现的可能性为4/6
故所求参赛方案有4∕6?A64=240种。
答案:240种。
十三、“树图”表示法
对某些分步进行的问题,可依次对每步可能出现的情况用“树”状图形表示出来。
例:四人各写出一张贺卡,先集中起来,然后每人从中拿一张别人送出的贺卡,则四张贺卡的不同分配方式有( )种。
A.6 B.9 C.11 D.32
分析:将四张贺卡分别记为A,B,C,D。由题意,某人(不妨设为A卡的供卡人)取卡有3种情况。因此将卡的不同分配方式分为三类,对于每一类,其它人依次取卡分步进行。为避免重复或遗漏现象,可用树状图表示。
↗A→D→C ↗A→D→B ↗A→B→C
B→C→D→A C→D→A→B D→C→A→B
↘D→A→C ↘D→B→A ↘C→B→A
所以共有9种不同的分配方式。
又或:分析:设4人为甲、乙、丙、丁,则甲送出的卡片可以且只可以由其他三人中的一人收到,故有3种分配方式。以乙收到为例,其他人收到卡片的情况可分为两类:第一类,甲收到乙送出的卡片,这时丙、丁只有互送卡片1种分配方式;第二类,甲收到的不是乙送出的卡片,这时,甲收到卡片的方式有2种(分别是丙或丁送出的),对每一种情况,丙、丁收到卡片的方式只有1种。因此,根据分步计数原理,不同的分配方式有:3×(1+2)=9(种)。
注意:解题的关键在第2个人和第3个人的拿法,只要给他们规定一个拿卡的顺序,依次进行,则根据分步计数原理即可求得。
例4. 把6棵不同的蔬菜,分别捆成3捆,在下列情况下,分别有多少分捆的方法?
⑴ 每捆2棵 ;⑵ 一捆3棵,一捆2棵,一捆1棵.
解:⑴ 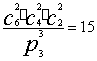 ⑵
⑵ 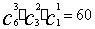
例5. 把6棵不同的菜,分别种在3块不同的土地上,在下列情况下,分别有多少种植方法?
⑴ 每块地上种2棵;
⑵ 甲地3棵,乙地2棵,丙地1棵;
⑶ 一块地上3棵,一块地上2棵,一块地上1棵.
解:⑴ 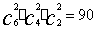

⑵ 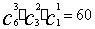
⑶ 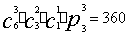
变式:如果是7棵不同的菜,种到3块土地上,一块地上3棵,一块地上2棵,还有一块地上2棵呢?
答案为 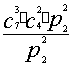
典型易错题:
例1 某天有六节不同的课,若第一节排数学,或第六节排体育,问共有多少种不同的排法?
错解 数学排第一节的排法有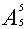 种,体育排第六节的排法也有
种,体育排第六节的排法也有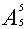 种,根据加法原理,第一节排数学或排体育的排法共有
种,根据加法原理,第一节排数学或排体育的排法共有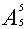 +
+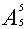 =2
=2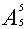 =240种
=240种
剖析 在数学排第一节的排法中,存在着体育排第六节的排法,在排体育第六节的排法中,存在着数学排第一节的排法,它重复计算了数学排第一节,同时体育排第六节的排法,即多算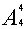 种。正确结果是:
种。正确结果是: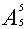 +
+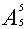 -
-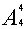 =216种
=216种
例2 从4名男生3名女生中选3人成立科技小组,问当选者中至少有一名男生和一名女生的选法有几种?
错解 先选一名男生,有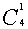 种选法,再选一名女生,有
种选法,再选一名女生,有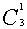 种选法,最后从余下的5名学生中选一名有
种选法,最后从余下的5名学生中选一名有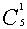 种选法,故共有选法
种选法,故共有选法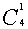
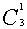
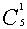 =60种
=60种
剖析 上述解法中,每一种选法都符合要求,但是否有重复计算呢?为此我们不妨设4名男生为A1,A2,A3,A4,3名女生为B1,B2,B3,把上面选法中含有一名男生的选法分为4类。在含有男生A1的一类的选法有:A1,B1,A2,即先选A1,再选B1,最后选A2;在含有男生A2的一类中有A2, B1,A1,即先选A2,再选B1,最后选A1。显然这两种选法被重复计算了。因此上述解法是错误的。错误的原因在于没有将符合要求的选法进行正确分类,分类要不重不漏。
正解 以男生人数分类,则符合条件的有且仅有两类,一类是男生一名女生两名,有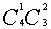 种选法,另一类是男生两名女生一名,有
种选法,另一类是男生两名女生一名,有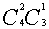 。故共有
。故共有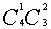 +
+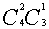 =30种
=30种
例3 n个不同的球放入n-1个不同的盒子,假设每个盒子都有足够大的容量,问每个盒子中至少有一个球的放法共有多少种?
错解 先在每盒子中放入一球共有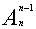 种放法,再将剩下的一球放入,有n-1种放法。由乘法原理,共有放法(n-1)
种放法,再将剩下的一球放入,有n-1种放法。由乘法原理,共有放法(n-1)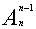 =(n-1)n!种.
=(n-1)n!种.
剖析 将这n个球和n-1个盒子均依次编号,设先在每盒中放入一球时,有一种放法是第I号盒子恰好放入第I号球,其中I=1,2,…,n-1,然后再考虑剩下的第n号球的放法,假设第n号球恰好放入第1号盒,这样,除1号盒中放有第一号与第n号两个球外,其余各盒均只放有一个与盒子同号的球,若先在每盒中放入一球时,第n号球恰好放入第1号盒,,而其余各盒所放的球均与盒子同号,这样,再将剩下的1号球放入盒中时,必有一种放法是恰好放入1号盒,这时,出现与前一次完全相同的结果,但在上面的解法中被当成两种不同的放法来计算,故重复。
正确的解法是:先从n个球中任取2个组成一组,共有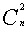 种方法;然后把这2个球当作1份,另外n-2个球每个球算1份,共有n-1份,把这n-1份分放在n-1个盒子中,且使每盒中恰有1份,共有
种方法;然后把这2个球当作1份,另外n-2个球每个球算1份,共有n-1份,把这n-1份分放在n-1个盒子中,且使每盒中恰有1份,共有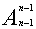 种放法,由乘法原理,符合题意的放法种数为
种放法,由乘法原理,符合题意的放法种数为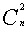
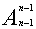 =
=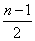 n!
n!
例4、将4个不同的球放入4个不同的盆子内
(1)共有几种放法?
(2)恰有一个盆子未放球,共几种放法?
(3)恰有一个盆子内有2球,共几种放法?
(4)恰有两个盆子内未放球,共有几种放法?
解题思路分析:
(1)把球作为研究对象,事件指所有球都放完。因每一只球都有四种放法,故由分步计数原理,共有44=256(种);
(2)问题即为“4个球放入三个盆子,每个盆子内都要放球,共有几种放法?”
第一步是把4只球分成2,1,1三组,共有C42种放法;
第二步把3组球放入三个盆子中去(作全排列),有A43种;
由分步计数原理,共有N=C42A43(种)
评注:第二步应是A43,而不是A33,因还要选从四个盆子中选三个盆子,然后作全排。
(3)仔细审题,认清问题的本质。“恰有一盆子内入2个球”即另三个盆子放2球,也即另外3个盆子恰有一个空盆,因此,“恰有一个盆子放2球”与“恰有一个盆子不放球”是等价的。
(4)先取走两个不放球的盆子,有C42种取法;其次将4球分两类放入所剩2盆;第一类均匀放入,有C42C22种放法;第二步按3,1分组放入,有C43C11A22种放法。故有
N=C42(C42C22+C43C11A22)=84(种)。
例5、用0,1,2,3,4五个数字组成各位数字不重复的五位数,若按由小到大排列,试问:(1)42130是第几个数?(2)第60个数是什么?
解题思路分析:(1)要知道42130是第几个数,只要知道比它小的有几个数,就基本解决了。根据数的大小比较的原则,比42130小的数可以分成如下几类:
1□□□□,2□□□□,3□□□□型的;
40□□□,41□□□型的;
420□□型的;
4200□型的。
各类的数分别有C31A44,C21A33,C11A22,C11A11个,所以比42130小的数有C31A44+C21A33+C11A22+C11A11=87个,42130是第88个。
(2)万位1的数,即1□□□□型的数,有A44=24个;
万位为2的,同样有A44=24个;
万位为3的也有24个,所以第60个数是万位为3的这一类数中的第12个数,再具体分类:
30□□□型的有A33=6个;
31□□□型的有A33=6个
所以,第12个数是31□□□型的数中最大的一个即为31420。
评注:此类题型称为字典式排列问题,解题的关键在于根据题意正确地进行分类,分类的关键是采用类似查字典的方法,从高位向低位,一位一位地考察各位上所取数字的可能性。
道路网走法的一般解法
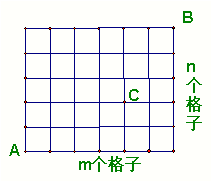
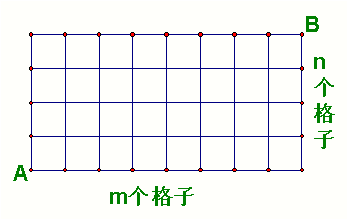 题目 图1是某城市道路网的局部,横向m个格子,纵向n个格子,若只允许向东或向北走,则从A处到B处有多少种不同的走法?
题目 图1是某城市道路网的局部,横向m个格子,纵向n个格子,若只允许向东或向北走,则从A处到B处有多少种不同的走法?
本题在很多资料中都能见到,其解法是把道路网简化成较少格子后分步求,或猜想出一般结论,而没有证明。下面用组合知识给出其一般性的推导过程及结论。
从A处到B处走每个格子的一边作为一步,则对于m×n的网格共走m+n步,我们把这m+n步看作m+n个位置。由于每种走法均为向东走了m步,向北走了n步,这样,当从m+n个位置中选出m个位置作为向东走的各种情形,有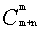 种选法,剩余n个位置为向北走,所有不同走法有
种选法,剩余n个位置为向北走,所有不同走法有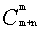 种。也可以这样计算:从m+n个位置中选n个作为向北走的各种情形,剩余m个位置为向东走。故所求的不同走法有
种。也可以这样计算:从m+n个位置中选n个作为向北走的各种情形,剩余m个位置为向东走。故所求的不同走法有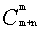 种。
种。
 例 :
例 :
图2是6×5的网格线图,只允许走网线,则从A经过C到B处的最短路线有多少条?
解 最短路线的走法只能向上或向右走,从A处到C处有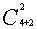 =
=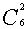 =15条。从C处到B处有
=15条。从C处到B处有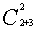 =
=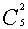 =10条。故满足题设的最短路线有15×10=150条。
=10条。故满足题设的最短路线有15×10=150条。

例:如图,从5×6方格中的顶点A到顶点B的最短线路有多少条?
分析:从A到的最短路线均需走11步,(一步即为一个单位),即横向走6步,纵向走5步,因此要确定一种走法,只需确定这11步中哪6步是横向走即可,
故不同的走法为C116=462种. 答案:462种。
-
排列组合方法总结
如果你希望成功,以恒心为良友,以经验为参谋,以小心为兄弟,以希望为哨兵排列组合方法总结(新导航用)1、【特殊元素、特殊位置】优先法…
-
排列组合的二十种解法(最全的排列组合方法总结)
一.例1.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.练习题:7种不同的花种在排成一列的花盆里,若两种葵花不种在中…
-
20xx-20xx MBA排列组合方法总结
排列组合【解题方法总结】一、【特殊元素、特殊位置】优先法在排列、组合问题中,如果某些元素或位置有特殊要求,则一般需要优先满足要求。…
-
排列组合方法总结
排列组合方法总结直接法例1:用1,2,3,4,5,6这6个数字组成无重复的四位数,试求满足下列条件的四位数各有多少个?1)数字1不…
-
排列组合问题解法总结
二十种排列组合问题的解法排列组合问题联系实际生动有趣,但题型多样,思路灵活,因此解决排列组合问题,首先要认真审题,弄清楚是排列问题…
-
20xx-20xx MBA排列组合方法总结
排列组合【解题方法总结】一、【特殊元素、特殊位置】优先法在排列、组合问题中,如果某些元素或位置有特殊要求,则一般需要优先满足要求。…
-
排列组合的二十种解法(最全的排列组合方法总结)
一.例1.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.练习题:7种不同的花种在排成一列的花盆里,若两种葵花不种在中…
-
排列组合方法总结
如果你希望成功,以恒心为良友,以经验为参谋,以小心为兄弟,以希望为哨兵排列组合方法总结(新导航用)1、【特殊元素、特殊位置】优先法…