导数题型总结
导数题型总结
题型一:利用导函数解析式求原函数解析式
例1:已知多项式函数 的导数
的导数 ,且
,且 ,求
,求
例2:已知多项式函数 为奇函数,
为奇函数, ,求
,求
例3:已知函数 为偶函数,它的图象过点
为偶函数,它的图象过点 ,且在
,且在 处的切线方程为
处的切线方程为 ,求
,求
题型二:求切线问题
例1:已知曲线方程为 ,则在点
,则在点 处切线的斜率为 ,切线的倾斜角为
处切线的斜率为 ,切线的倾斜角为
例2:求曲线 在原点处的切线方程
在原点处的切线方程
切线斜率不存在所以切线方程为
例3:求曲线 在点
在点 出的切线与X轴,直线
出的切线与X轴,直线 所围成的三角形的面积
所围成的三角形的面积
切线方程为 三角形面积
三角形面积
例4:求曲线 分别满足下列条件的切线方程
分别满足下列条件的切线方程
(1)平行于直线 (2)垂直于直线
(2)垂直于直线
(3)与X轴成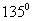 的倾斜角 (4)过点
的倾斜角 (4)过点 ,且与曲线相切的直线
,且与曲线相切的直线
例5:已知函数 在R上满足
在R上满足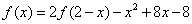 ,则曲线
,则曲线
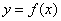 在点
在点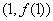 处的切线方程是
处的切线方程是
例6:已知函数 在R上满足
在R上满足 ,则曲线
,则曲线
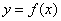 在点
在点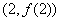 处的切线方程是
处的切线方程是
题型三:求倾斜角
例1:P在曲线 上移动,在点P处的切线的倾斜角为α,则α的取值范围是______
上移动,在点P处的切线的倾斜角为α,则α的取值范围是______
例2:.曲线 在点
在点 处的切线倾斜角为__________;
处的切线倾斜角为__________;
题型四:导数与函数图像问题
例1:若函数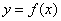 的导函数在区间
的导函数在区间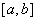 上是增函数,则函数
上是增函数,则函数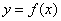 在
在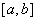 上的图象可能是 ( )
上的图象可能是 ( )

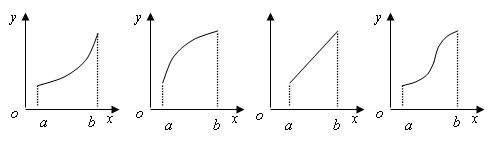

A . B. C. D..
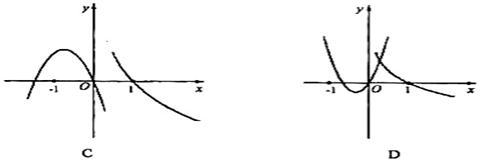
例2函数y=ax2+ bx与y= 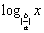 (ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是( )
(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是( )

例3函数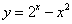 的图像大致是( )
的图像大致是( )
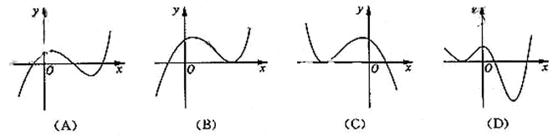
例4设 是函数
是函数 的导函数,将
的导函数,将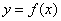 和
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )

例5设 是函数
是函数 的导函数,
的导函数, 的图象如下图(1)所示,则
的图象如下图(1)所示,则 的图象最有可能的是
的图象最有可能的是





例6.设函数f(x)在定义域内可导,y=f(x)的图象如图1所示,则导函数y=f ¢(x)可能为 ( )


题型五:结合单调性求参数的取值范围
例1:若函数 为R上的增函数,则实数
为R上的增函数,则实数 满足的条件是
满足的条件是
例2:已知函数 在R是单调函数,则实数
在R是单调函数,则实数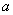 的取值范围是
的取值范围是
例3:已知函数 在区间
在区间 上是减函数,则
上是减函数,则 的取值范围是
的取值范围是
例4:已知向量 ,
, ,若函数
,若函数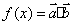 在区间
在区间 上是增函数,求t 的取值范围
上是增函数,求t 的取值范围
例5:已知函数 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数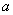 的取值范围是
的取值范围是
例6:若函数 有三个单调区间,则b 的取值范围是
有三个单调区间,则b 的取值范围是 
例7:设函数
(1)求 的单调区间和极值
的单调区间和极值
(2)若关于 的方程
的方程 有三个不同实根,求a 的取值范围
有三个不同实根,求a 的取值范围
(3)已知当 时,
时, 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
例8:已知 在
在 时取得极值
时取得极值
(1)求 的值
的值
(2)若对 ,
, 恒成立,求c 的取值范围
恒成立,求c 的取值范围
例9:已知函数 的图象与函数
的图象与函数 的图象关于点
的图象关于点 对称
对称
(1)求函数 的解析式
的解析式
(2)若 ,且
,且 在区间
在区间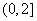 上是减函数求实数a 的取值范围
上是减函数求实数a 的取值范围
题型六:求单调区间
例1:(1)  (2)
(2) (3)
(3) 
例2:已知函数 的两个极值点是
的两个极值点是 和3 ,且
和3 ,且 ,
, ,求函数
,求函数 的解析式
的解析式
例3:已知 是三次函数,
是三次函数, 是一次函数,
是一次函数, ,
, 在
在 处有极值2 ,求
处有极值2 ,求 的解析式和单调区间
的解析式和单调区间
题型七:求极值问题
例1.(本小题满分12分)设函数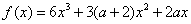 .(1)若
.(1)若 的两个极值点为
的两个极值点为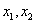 ,且
,且 ,求实数
,求实数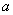 的值;(2)是否存在实数
的值;(2)是否存在实数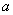 ,使得
,使得 是
是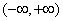 上的单调函数?若存在,求出
上的单调函数?若存在,求出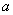 的值;若不存在,说明理由.
的值;若不存在,说明理由.
例2设函数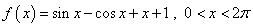 ,求
,求 的单调区间与极值.
的单调区间与极值.
例3已知函数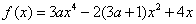
(I)当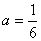 时,求
时,求 的极值;
的极值;
(II)若 在
在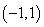 上是增函数,求
上是增函数,求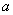 的取值范围
的取值范围
例4设定函数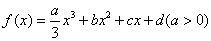 ,且方程
,且方程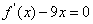 的两个根分别为1,4。
的两个根分别为1,4。
(Ⅰ)当a=3且曲线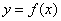 过原点时,求
过原点时,求 的解析式;
的解析式;
(Ⅱ)若 在
在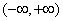 无极值点,求a的取值范围。
无极值点,求a的取值范围。
题型八:最值与参数问题
例1:求抛物线 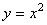 上的点到直线
上的点到直线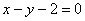 的最短距离.
的最短距离.
例2:已知函数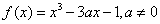
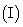 求
求 的单调区间;
的单调区间;
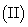 若
若 在
在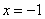 处取得极值,求
处取得极值,求 的最值。
的最值。
例3;已知函数 图象上一点
图象上一点 处的切线斜率为
处的切线斜率为 ,
,

(Ⅰ)求 的值;
的值;
(Ⅱ)当 时,求
时,求 的值域;
的值域;
(Ⅲ)当 时,不等式
时,不等式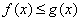 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
例4、已知函数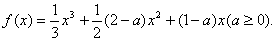
(I)求 的单调区间;
的单调区间;
(II)若 在[0,1]上单调递增,求a的取值范围。
在[0,1]上单调递增,求a的取值范围。
例5、已知函数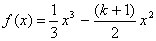 ,
,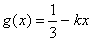 ,且
,且 在区间
在区间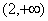 上为增函数.
上为增函数.
(1) 求实数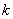 的取值范围;
的取值范围;
(2) 若函数 与
与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数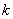 的取值范围.
的取值范围.
例6、

例7、已知函数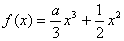 ,
,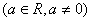 (1)求
(1)求 的单调区间;(2)令
的单调区间;(2)令 =
=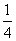 x4+f(x)(x∈R)有且仅有3个极值点,求a的取值范围.
x4+f(x)(x∈R)有且仅有3个极值点,求a的取值范围.
例8已知函数 的切线方程为y=3x+1
的切线方程为y=3x+1
(Ⅰ)若函数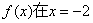 处有极值,求
处有极值,求 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,求函数 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(Ⅲ)若函数 在区间[-2,1]上单调递增,求实数b的取值范围
在区间[-2,1]上单调递增,求实数b的取值范围
例9:已知三次函数 在
在 和
和 时取极值,且
时取极值,且 .
.
(1) 求函数 的表达式;
的表达式;
(2) 求函数 的单调区间和极值;
的单调区间和极值;
(3) 若函数 在区间
在区间 上的值域为
上的值域为 ,试求
,试求 、
、 应满足的条件.
应满足的条件.
例10:已知函数 在
在 处取得极值,
处取得极值,
(1)用 表示
表示 ;
;
(2)设函数 如果
如果 在区间
在区间 上存在极小值,求实数
上存在极小值,求实数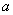 的取值范围.
的取值范围.
例11:已知
(1)当 时, 求证
时, 求证 在
在 内是减函数;
内是减函数;
(2)若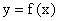 在
在 内有且只有一个极值点, 求a的取值范围.
内有且只有一个极值点, 求a的取值范围.
例12:设函数
(1)求函数 的单调区间、极值.
的单调区间、极值.
(2)若当 时,恒有
时,恒有 ,试确定a的取值范围.
,试确定a的取值范围.
例13:(2006全国卷)设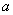 为实数,函数
为实数,函数 在
在 和
和 都是增函数,求
都是增函数,求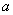 的取值范围。
的取值范围。
例14.(20##年江西卷)已知函数f(x)=x3+ax2+bx+c在x=- 与x=1时都取得极值
与x=1时都取得极值
(1)求a、b的值与函数f(x)的单调区间
(2)若对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
例15.已知函数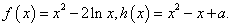
(Ⅰ)求函数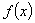 的极值;
的极值;
(Ⅱ)设函数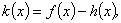 若函数
若函数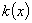 在
在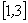 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 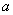 的取值范围.
的取值范围.
例16.(本小题满分14分)已知函数f(x)=kx3-3x2+1(k≥0).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)的极小值大于0, 求k的取值范围.
第二篇:导数常见题型及知识点分析(名师总结)
第一部分:导数的运算法则及基本公式应用
重难点归纳
1 深刻理解导数的概念,了解用定义求简单的导数
深刻理解导数的概念,了解用定义求简单的导数
 表示函数的平均改变量,它是Δx的函数,而f′(x0)表示一个数值,即f′(x)=
表示函数的平均改变量,它是Δx的函数,而f′(x0)表示一个数值,即f′(x)= ,知道导数的等价形式
,知道导数的等价形式
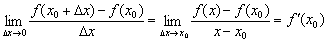

2 求导其本质是求极限,在求极限的过程中,力求使所求极限的结构形式转化为已知极限的形式,即导数的定义,这是顺利求导的关键
求导其本质是求极限,在求极限的过程中,力求使所求极限的结构形式转化为已知极限的形式,即导数的定义,这是顺利求导的关键
3 对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误
对于函数求导,一般要遵循先化简,再求导的基本原则,求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用,在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误
4 复合函数求导法则,像链条一样,必须一环一环套下去,而不能丢掉其中的一环
复合函数求导法则,像链条一样,必须一环一环套下去,而不能丢掉其中的一环 必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的,分清其间的复合关系
必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的,分清其间的复合关系
典型题例示范讲解
例1求函数的导数

命题意图 本题3个小题分别考查了导数的四则运算法则,复合函数求导的方法,以及抽象函数求导的思想方法
本题3个小题分别考查了导数的四则运算法则,复合函数求导的方法,以及抽象函数求导的思想方法 这是导数中比较典型的求导类型
这是导数中比较典型的求导类型
知识依托 解答本题的闪光点是要分析函数的结构和特征,挖掘量的隐含条件,将问题转化为基本函数的导数
解答本题的闪光点是要分析函数的结构和特征,挖掘量的隐含条件,将问题转化为基本函数的导数
错解分析 本题难点在求导过程中符号判断不清,复合函数的结构分解为基本函数出差错
本题难点在求导过程中符号判断不清,复合函数的结构分解为基本函数出差错
技巧与方法 先分析函数式结构,找准复合函数的式子特征,按照求导法则进行求导
先分析函数式结构,找准复合函数的式子特征,按照求导法则进行求导
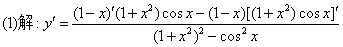

(2)解 y=μ3,μ=ax-bsin2ωx,μ=av-by v=x,y=sinγ γ=ωx
y=μ3,μ=ax-bsin2ωx,μ=av-by v=x,y=sinγ γ=ωx
y′=(μ3)′=3μ2·μ′=3μ2(av-by)′=3μ2(av′-by′)=3μ2(av′-by′γ′)
=3(ax-bsin2ωx)2(a-bωsin2ωx)
(3)解法一 设y=f(μ),μ=
设y=f(μ),μ=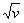 ,v=x2+1,则y′x=y′μμ′v·v′x=f′(μ)·
,v=x2+1,则y′x=y′μμ′v·v′x=f′(μ)· v-
v- ·2x
·2x
=f′(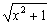 )·
)·
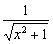 ·2x=
·2x=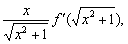
解法二 y′=[f(
y′=[f(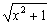 )]′=f′(
)]′=f′(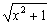 )·(
)·(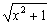 )′=f′(
)′=f′(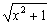 )·
)· (x2+1)
(x2+1)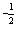 ·(x2+1)′
·(x2+1)′
=f′(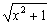 )·
)· (x2+1)
(x2+1) 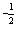 ·2x=
·2x= f′(
f′(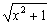 )
)
例2利用导数求和
(1)Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N*)
(2)Sn=C +2C
+2C +3C
+3C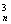 +…+nC
+…+nC ,(n∈N*)
,(n∈N*)
命题意图 培养考生的思维的灵活性以及在建立知识体系中知识点灵活融合的能力
培养考生的思维的灵活性以及在建立知识体系中知识点灵活融合的能力
知识依托 通过对数列的通项进行联想,合理运用逆向思维
通过对数列的通项进行联想,合理运用逆向思维 由求导公式(xn)′=nxn-1,可联想到它们是另外一个和式的导数
由求导公式(xn)′=nxn-1,可联想到它们是另外一个和式的导数 关键要抓住数列通项的形式结构
关键要抓住数列通项的形式结构
错解分析 本题难点是考生易犯思维定势的错误,受此影响而不善于联想
本题难点是考生易犯思维定势的错误,受此影响而不善于联想
技巧与方法 第(1)题要分x=1和x≠1讨论,等式两边都求导
第(1)题要分x=1和x≠1讨论,等式两边都求导
解 (1)当x=1时Sn=1+2+3+…+n=
(1)当x=1时Sn=1+2+3+…+n= n(n+1);
n(n+1);
当x≠1时,∵x+x2+x3+…+xn= ,
,
两边都是关于x的函数,求导得(x+x2+x3+…+xn)′=( )′
)′
即Sn=1+2x+3x2+…+nxn-1=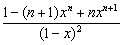
(2)∵(1+x)n=1+C x+C
x+C x2+…+C
x2+…+C xn,两边都是关于x的可导函数,求导得
xn,两边都是关于x的可导函数,求导得
n(1+x)n-1=C +2C
+2C x+3C
x+3C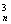 x2+…+nC
x2+…+nC xn-1,令x=1得,n·2n-1=C
xn-1,令x=1得,n·2n-1=C +2C
+2C +3C
+3C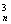 +…+nC
+…+nC ,
,
即Sn=C +2C
+2C +…+nC
+…+nC =n·2n-1
=n·2n-1
学生巩固练习
1 y=esinxcos(sinx),则y′(0)等于( )
y=esinxcos(sinx),则y′(0)等于( )
A 0 B
0 B 1 C
1 C -1 D
-1 D 2
2
2 经过原点且与曲线y=
经过原点且与曲线y=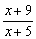 相切的方程是( )
相切的方程是( )
A x+y=0或
x+y=0或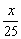 +y=0 B
+y=0 B x-y=0或
x-y=0或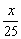 +y=0
+y=0
C x+y=0或
x+y=0或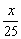 -y=0 D
-y=0 D x-y=0或
x-y=0或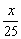 -y=0
-y=0
3 若f′(x0)=2,
若f′(x0)=2,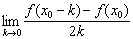 =_________
=_________
4 设f(x)=x(x+1)(x+2)…(x+n),则f′(0)=_________
设f(x)=x(x+1)(x+2)…(x+n),则f′(0)=_________
5 已知曲线C1:y=x2与C2:y=-(x-2)2,直线l与C1、C2都相切,求直线l的方程
已知曲线C1:y=x2与C2:y=-(x-2)2,直线l与C1、C2都相切,求直线l的方程
6 求函数的导数
求函数的导数
(1)y=(x2-2x+3)e2x;
(2)y=

7 有一个长度为5 m的梯子贴靠在笔直的墙上,假设其下端沿地板以3 m/s的速度离开墙脚滑动,求当其下端离开墙脚1
有一个长度为5 m的梯子贴靠在笔直的墙上,假设其下端沿地板以3 m/s的速度离开墙脚滑动,求当其下端离开墙脚1 4 m时,梯子上端下滑的速度
4 m时,梯子上端下滑的速度
8 求和Sn=12+22x+32x2+…+n2xn-1,(x≠0,n∈N*)
求和Sn=12+22x+32x2+…+n2xn-1,(x≠0,n∈N*)
参考答案
1 解析
解析 y′=esinx[cosxcos(sinx)-cosxsin(sinx)],y′(0)=e0(1-0)=1答案
y′=esinx[cosxcos(sinx)-cosxsin(sinx)],y′(0)=e0(1-0)=1答案 B
B
2 解析
解析 设切点为(x0,y0),则切线的斜率为k=
设切点为(x0,y0),则切线的斜率为k=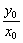 ,另一方面,y′=(
,另一方面,y′=(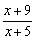 )′=
)′=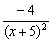 ,
,
故y′(x0)=k,即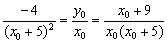 或x02+18x0+45=0
或x02+18x0+45=0
得x0(1)=-3, x0 (2)=-15,对应有y0(1)=3,y0(2)=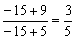 ,因此得两个切点A(-3,3)或B(-15,
,因此得两个切点A(-3,3)或B(-15,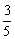 ),
),
从而得y′(A)=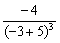 =-1及y′(B)=
=-1及y′(B)=  ,
,
由于切线过原点,故得切线 lA:y=-x或lB:y=-
lA:y=-x或lB:y=-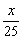
 答案
答案 A
A
3 解析
解析 根据导数的定义
根据导数的定义
f′(x0)= (这时
(这时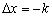 )
)
答案 -1
-1
4 解析
解析 设g(x)=(x+1)(x+2)……(x+n),则f(x)=xg(x),
设g(x)=(x+1)(x+2)……(x+n),则f(x)=xg(x),
于是f′(x)=g(x)+xg′(x),f′(0)=g(0)+0·g′(0)=g(0)=1·2·…n=n!答案 n!
n!
5 解
解 设l与C1相切于点P(x1,x12),与C2相切于Q(x2,-(x2-2)2)
设l与C1相切于点P(x1,x12),与C2相切于Q(x2,-(x2-2)2)
对于C1 y′=2x,则与C1相切于点P的切线方程为
y′=2x,则与C1相切于点P的切线方程为
y-x12=2x1(x-x1),即y=2x1x-x12 ①
对于C2 y′=-2(x-2),与C2相切于点Q的切线方程为
y′=-2(x-2),与C2相切于点Q的切线方程为
y+(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4 ②
∵两切线重合,∴2x1=-2(x2-2)且-x12=x22-4,
解得x1=0,x2=2或x1=2,x2=0∴直线l方程为y=0或y=4x-4
6 解
解 (1)注意到y>0,两端取对数,得
(1)注意到y>0,两端取对数,得
lny=ln(x2-2x+3)+lne2x=ln(x2-2x+3)+2x
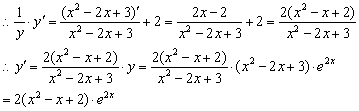
(2)两端取对数,得
ln|y|=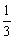 (ln|x|-ln|1-x|),
(ln|x|-ln|1-x|),
两边解x求导,得

7 解
解 设经时间t秒梯子上端下滑s米,则s=5-
设经时间t秒梯子上端下滑s米,则s=5- ,
,
当下端移开1 4 m时,t0=
4 m时,t0=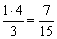 ,又s′=-
,又s′=- (25-9t2)
(25-9t2)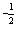 ·(-9·2t)=9t
·(-9·2t)=9t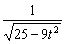 ,
,
所以s′(t0)=9×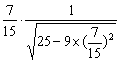 =0
=0 875(m/s)
875(m/s)
8 解
解 (1)当x=1时,Sn=12+22+32+…+n2=
(1)当x=1时,Sn=12+22+32+…+n2= n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1=
n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1= ,
,
两边同乘以x,得x+2x2+3x2+…+nxn=
两边对x求导,得Sn=12+22x2+32x2+…+n2xn-1=
第二部分:用导数求切线方程的四种类型
求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出切点 及斜率,其求法为:设
及斜率,其求法为:设 是曲线
是曲线 上的一点,则以
上的一点,则以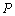 的切点的切线方程为:
的切点的切线方程为: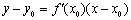 .若曲线
.若曲线 在点
在点 的切线平行于
的切线平行于 轴(即导数不存在)时,由切线定义知,切线方程为
轴(即导数不存在)时,由切线定义知,切线方程为 .
.
下面例析四种常见的类型及解法.
类型一:已知切点,求曲线的切线方程
此类题较为简单,只须求出曲线的导数 ,并代入点斜式方程即可.
,并代入点斜式方程即可.
例1 曲线 在点
在点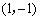 处的切线方程为( )
处的切线方程为( )
A.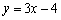 B.
B.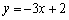 C.
C. D.
D.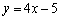
解:由 则在点
则在点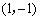 处斜率
处斜率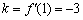 ,故所求的切线方程为
,故所求的切线方程为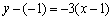 ,即
,即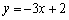 ,因而选B.
,因而选B.
例2 已知曲线C y=x3-3x2+2x,直线l:y=kx,且l与C切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标
y=x3-3x2+2x,直线l:y=kx,且l与C切于点(x0,y0)(x0≠0),求直线l的方程及切点坐标
解 由l过原点,知k=
由l过原点,知k=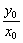 (x0≠0),点(x0,y0)在曲线C上,y0=x03-3x02+2x0,
(x0≠0),点(x0,y0)在曲线C上,y0=x03-3x02+2x0,
∴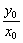 =x02-3x0+2y′=3x2-6x+2,k=3x02-6x0+2又k=
=x02-3x0+2y′=3x2-6x+2,k=3x02-6x0+2又k=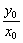 ,∴3x02-6x0+2=x02-3x0+2
,∴3x02-6x0+2=x02-3x0+2
2x02-3x0=0,∴x0=0或x0=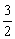 由x≠0,知x0=
由x≠0,知x0=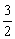
∴y0=(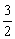 )3-3(
)3-3(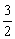 )2+2·
)2+2·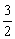 =-
=- ∴k=
∴k=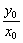 =-
=-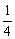 ∴l方程y=-
∴l方程y=-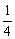 x 切点(
x 切点(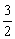 ,-
,- )
)
类型二:已知斜率,求曲线的切线方程
此类题可利用斜率求出切点,再用点斜式方程加以解决.
例3 与直线 的平行的抛物线
的平行的抛物线 的切线方程是( )
的切线方程是( )
A. B.
B. C.
C. D.
D.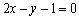
解:设 为切点,则切点的斜率为
为切点,则切点的斜率为 .
. .
.
由此得到切点 .故切线方程为
.故切线方程为 ,即
,即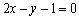 ,故选D.
,故选D.
评注:此题所给的曲线是抛物线,故也可利用 法加以解决,即设切线方程为
法加以解决,即设切线方程为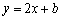 ,代入
,代入 ,得
,得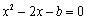 ,又因为
,又因为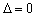 ,得
,得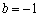 ,故选D.
,故选D.
类型三:已知过曲线上一点,求切线方程
过曲线上一点的切线,该点未必是切点,故应先设切点,再求切点,即用待定切点法.
例4 求过曲线 上的点
上的点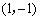 的切线方程.
的切线方程.
解:设想 为切点,则切线的斜率为
为切点,则切线的斜率为 .
. 切线方程为
切线方程为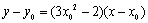 .
.
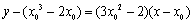 .又知切线过点
.又知切线过点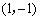 ,把它代入上述方程,
,把它代入上述方程,
得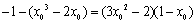 .解得
.解得 ,或
,或 .
.
故所求切线方程为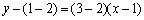 ,或
,或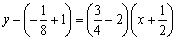 ,即
,即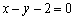 ,或
,或 .
.
评注:可以发现直线 并不以
并不以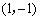 为切点,实际上是经过了点
为切点,实际上是经过了点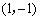 且以
且以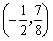 为切点的直线.这说明过曲线上一点的切线,该点未必是切点,解决此类问题可用待定切点法.
为切点的直线.这说明过曲线上一点的切线,该点未必是切点,解决此类问题可用待定切点法.
类型四:已知过曲线外一点,求切线方程
此类题可先设切点,再求切点,即用待定切点法来求解.
例5 求过点 且与曲线
且与曲线 相切的直线方程.
相切的直线方程.
解:设 为切点,则切线的斜率为
为切点,则切线的斜率为 .
. 切线方程为
切线方程为 ,
,
即 .又已知切线过点
.又已知切线过点 ,把它代入上述方程,得
,把它代入上述方程,得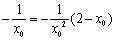 .
.
解得 ,即
,即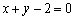 .
.
评注:点 实际上是曲线外的一点,但在解答过程中却无需判断它的确切位置,充分反映出待定切点法的高效性.
实际上是曲线外的一点,但在解答过程中却无需判断它的确切位置,充分反映出待定切点法的高效性.
例6 已知函数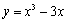 ,过点
,过点 作曲线
作曲线 的切线,求此切线方程.
的切线,求此切线方程.
解:曲线方程为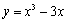 ,点
,点 不在曲线上.设切点为
不在曲线上.设切点为 ,
,
则点 的坐标满足
的坐标满足 .因
.因 ,
,
故切线的方程为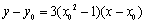 .
.
点 在切线上,则有
在切线上,则有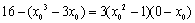 .化简得
.化简得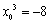 ,解得
,解得 .
.
所以,切点为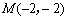 ,切线方程为
,切线方程为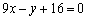 .
.
评注:此类题的解题思路是,先判断点A是否在曲线上,若点A在曲线上,化为类型一或类型三;若点A不在曲线上,应先设出切点并求出切点.
第三部分:导数的应用 最大值与最小值
一、教学内容
导数的应用 最大值与最小值
一般地,在闭区间 上连续的函数
上连续的函数 在
在 上必有最大值与最小值;在开区间
上必有最大值与最小值;在开区间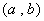 内连续的函数
内连续的函数 不一定有最大值与最小值,例如
不一定有最大值与最小值,例如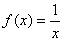 在
在 内的图象连续,但无最大值和最小值。
内的图象连续,但无最大值和最小值。
设函数 在
在 上连续,在
上连续,在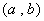 内可导,求
内可导,求 在
在 上的最大值与最小值的步骤如下:
上的最大值与最小值的步骤如下:
(1)求 在
在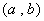 内的极值;
内的极值;
(2)将 的各极值与
的各极值与 ,
,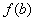 比较,其中最大的一个是最大值,最小的一个是最小值。
比较,其中最大的一个是最大值,最小的一个是最小值。
二、【典型例题】
[例1] 求函数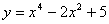 在区间
在区间 上的最大值与最小值。
上的最大值与最小值。
解: ,令
,令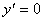 ,有
,有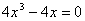

当 变化时,
变化时,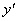 ,
,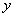 的变化情况如下表:
的变化情况如下表:

从上表可知,函数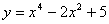 在区间
在区间 上最大值为13,最小值为4,利用此表可画出函数的图象如下:
上最大值为13,最小值为4,利用此表可画出函数的图象如下:

[例2] 已知 ,
, 的最大值为3,最小值
的最大值为3,最小值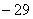 ,求
,求 、
、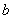 的值。
的值。
解:依题意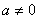 ,否则
,否则 与已知矛盾
与已知矛盾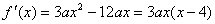 令
令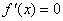 解得
解得 或
或 (1)当
(1)当 时,由
时,由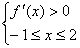 解得
解得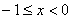
令 ,解得
,解得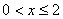 ,列表如下:
,列表如下:

由 连续,则当
连续,则当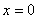 时,
时, 有最大值,即
有最大值,即 ,又由
,又由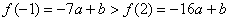 ,则
,则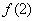 为最小值,故
为最小值,故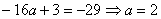 所以,当
所以,当 时,
时,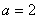 ,
,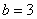
(2)当 时,列表如下:
时,列表如下:

故 最小值为
最小值为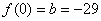 ,
, 最大值为
最大值为
所以,当 时,
时,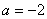 ,
,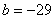
[例3] 已知两个函数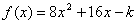 ,
,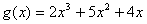 ,其中
,其中
(1)对任意的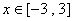 ,都有
,都有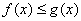 成立,求
成立,求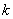 的取值范围。
的取值范围。
(2)对任意的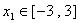 ,
,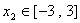 都有
都有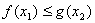 ,求
,求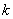 的取值范围。
的取值范围。
解:(1)设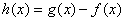 ,则对任意的
,则对任意的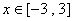 ,都有
,都有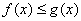 成立
成立
 ,
,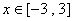 ,
,
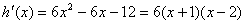 ,令
,令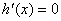 ,则
,则 或
或 ,列表如下:
,列表如下:

由上表可知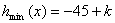 则
则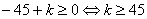
(2)对任意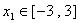 ,
,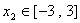 都有
都有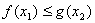 成立
成立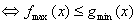 ,
,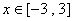
先求 ,
,
令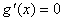 得
得 或
或 ,列表如下:
,列表如下:

则
再求 的最大值,
的最大值,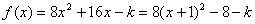 ,
,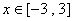 ,
,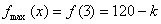 ,于是
,于是
[例4] 如图,在二次曲线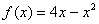 的图象与
的图象与 轴所围成的图形中有一个内接矩形,求这个矩形的最大面积
轴所围成的图形中有一个内接矩形,求这个矩形的最大面积

解:设点B坐标 ,则点C坐标为
,则点C坐标为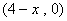
 ,
,
矩形ABCD的面积为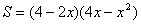
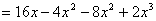

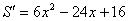 令
令 得
得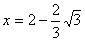 故当
故当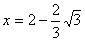 时,有S最大值为
时,有S最大值为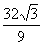
【模拟试题】(答题时间:30分钟)
1. 函数 (
( )在
)在 的最大值为5,最小值为
的最大值为5,最小值为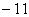 ,求
,求 的解析式。
的解析式。
2. 已知函数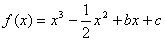 (1)若
(1)若 在
在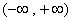 上是增函数,求b的取值范围。
上是增函数,求b的取值范围。
(2)若 在
在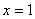 时取得极值,且
时取得极值,且 时,
时, 恒成立,求
恒成立,求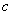 的取值范围。
的取值范围。
3. 用总长14.8m的钢条制做一个长方形容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容积最大?并求出它的最大容积?
【试题答案】
1. 解: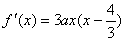

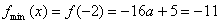 解之得
解之得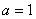 ,
,
故解析式为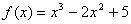

2. 解: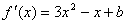
(1) 在
在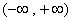 上是增函数
上是增函数 恒成立
恒成立
(2)易求得,当 时,
时,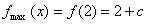
 恒成立
恒成立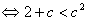
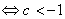 或
或
3. 解:设容器底面边长为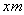 ,则另一边长为
,则另一边长为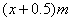 ,高为
,高为
=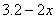 则容器容积为
则容器容积为
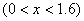
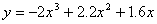
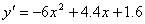
令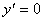 有
有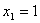 ,
,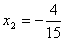 (舍),故当
(舍),故当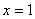 时,
时,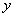 有最大值,
有最大值, ,此时高为1.2。
,此时高为1.2。
答:高为1.2m时,容积最大为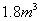 。
。
第四部分:利用导数证明不等式的常见题型
技巧精髓
1、利用导数研究函数的单调性,再由单调性来证明不等式是函数、导数、不等式综合中的一个难点,也是近几年高考的热点。
2、解题技巧是构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性或求最值,从而证得不等式,而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键。
一、利用题目所给函数证明
例1.已知函数 ,求证:当
,求证:当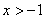 时,恒有
时,恒有
分析:本题是双边不等式,其右边直接从已知函数证明,左边构造函数 ,从其导数入手即可证明。
,从其导数入手即可证明。
【绿色通道】
∴当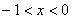 时,
时,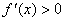 ,即
,即 在
在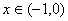 上为增函数
上为增函数
当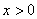 时,
时, ,即
,即 在
在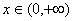 上为减函数
上为减函数
故函数 的单调递增区间为
的单调递增区间为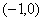 ,单调递减区间
,单调递减区间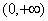
于是函数 在
在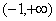 上的最大值为
上的最大值为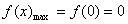 ,因此,当
,因此,当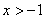 时,
时,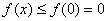 ,即
,即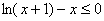 ∴
∴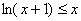 (右面得证),
(右面得证),
现证左面,令 ,
, 
当 ,
,
即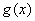 在
在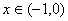 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,
故函数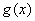 在
在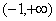 上的最小值为
上的最小值为 ,
,
∴ 当
当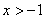 时,
时,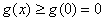 ,即
,即
∴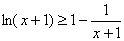 ,综上可知,当
,综上可知,当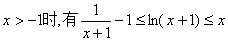
【警示启迪】如果 是函数
是函数 在区间上的最大(小)值,则有
在区间上的最大(小)值,则有
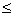
 (或
(或
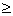
 ),那么要证不等式,只要求函数的最大值不超过
),那么要证不等式,只要求函数的最大值不超过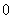 就可得证.
就可得证.
2、直接作差构造函数证明
例2已知函数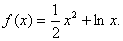 求证:在区间
求证:在区间 上,函数
上,函数 的图象在函数
的图象在函数 的图象的下方;
的图象的下方;
分析:函数 的图象在函数
的图象在函数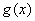 的图象的下方
的图象的下方 问题,
问题,
即 ,只需证明在区间
,只需证明在区间 上,恒有
上,恒有 成立,设
成立,设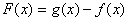 ,
,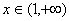 ,考虑到
,考虑到
要证不等式转化变为:当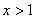 时,
时,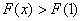 ,这只要证明:
,这只要证明: 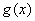 在区间
在区间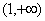 是增函数即可。
是增函数即可。
【绿色通道】设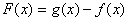 ,即
,即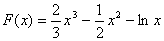 ,则
,则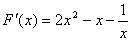 =
= 当
当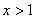 时,
时,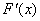 =
=
从而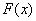 在
在 上为增函数,∴
上为增函数,∴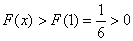
∴当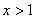 时
时 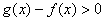 ,即
,即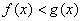 ,
,
故在区间 上,函数
上,函数 的图象在函数
的图象在函数 的图象的下方。
的图象的下方。
【警示启迪】本题首先根据题意构造出一个函数(可以移项,使右边为零,将移项后的左式设为函数),并利用导数判断所设函数的单调性,再根据函数单调性的定义,证明要证的不等式。读者也可以设 做一做,深刻体会其中的思想方法。
做一做,深刻体会其中的思想方法。
3、换元后作差构造函数证明
【例3】(20##年,山东卷)证明:对任意的正整数n,不等式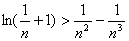 都成立.
都成立.
分析:本题是山东卷的第(II)问,从所证结构出发,只需令 ,则问题转化为:当
,则问题转化为:当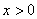 时,恒有
时,恒有 成立,现构造函数
成立,现构造函数 ,求导即可达到证明。
,求导即可达到证明。
【绿色通道】令 ,则
,则 在
在 上恒正,所以函数
上恒正,所以函数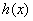 在
在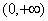 上单调递增,∴
上单调递增,∴ 时,恒有
时,恒有
即 ,∴
,∴
对任意正整数n,取
【警示启迪】我们知道,当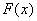 在
在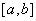 上单调递增,则
上单调递增,则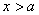 时,有
时,有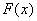
 .如果
.如果 =
=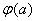 ,要证明当
,要证明当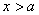 时,
时,
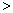
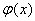 ,那么,只要令
,那么,只要令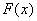 =
= -
-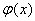 ,就可以利用
,就可以利用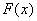 的单调增性来推导.也就是说,在
的单调增性来推导.也就是说,在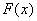 可导的前提下,只要证明
可导的前提下,只要证明
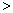 0即可.
0即可.
4、从条件特征入手构造函数证明
【例4】若函数y= 在R上可导且满足不等式x
在R上可导且满足不等式x >-
>- 恒成立,且常数a,b满足a>b,求证:.a
恒成立,且常数a,b满足a>b,求证:.a >b
>b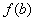
【绿色通道】由已知 x +
+ >0 ∴构造函数
>0 ∴构造函数 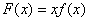 , 则
, 则 x
x +
+ >0, 从而
>0, 从而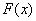 在R上为增函数。
在R上为增函数。
 ∴
∴ 即 a
即 a >b
>b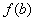
【警示启迪】由条件移项后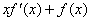 ,容易想到是一个积的导数,从而可以构造函数
,容易想到是一个积的导数,从而可以构造函数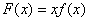 ,求导即可完成证明。若题目中的条件改为
,求导即可完成证明。若题目中的条件改为 ,则移项后
,则移项后 ,要想到是一个商的导数的分子,平时解题多注意总结。
,要想到是一个商的导数的分子,平时解题多注意总结。
【思维挑战】
1、(20##年,安徽卷) 设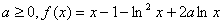 求证:当
求证:当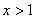 时,恒有
时,恒有 ,
,
2、(20##年,安徽卷)已知定义在正实数集上的函数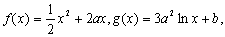 其中a>0,且
其中a>0,且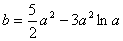 , 求证:
, 求证:
3、已知函数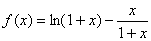 ,求证:对任意的正数
,求证:对任意的正数 、
、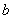 , 恒有
, 恒有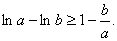
4、(20##年,陕西卷) 是定义在(0,+∞)上的非负可导函数,且满足
是定义在(0,+∞)上的非负可导函数,且满足 ≤0,对任意正数a、b,若a < b,则必有 ( )
≤0,对任意正数a、b,若a < b,则必有 ( )
(A)af (b)≤bf (a) (B)bf (a)≤af (b)
(C)af (a)≤f (b) (D)bf (b)≤f (a)
【答案咨询】
1、提示: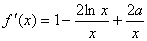 ,当
,当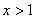 ,
,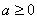 时,不难证明
时,不难证明
∴
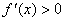 ,即
,即 在
在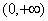 内单调递增,故当
内单调递增,故当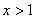 时,
时,
 ,∴当
,∴当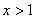 时,恒有
时,恒有
2、提示:设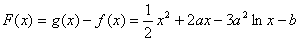 则
则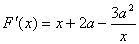
=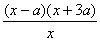


 ,∴ 当
,∴ 当 时,
时, ,
,
故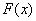 在
在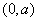 上为减函数,在
上为减函数,在 上为增函数,于是函数
上为增函数,于是函数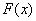 在
在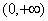 上的最小值是
上的最小值是 ,故当
,故当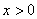 时,有
时,有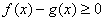 ,即
,即
3、提示:函数 的定义域为
的定义域为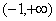 ,
,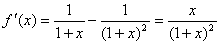
∴当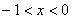 时,
时, ,即
,即 在
在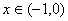 上为减函数
上为减函数
 当
当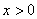 时,
时,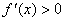 ,即
,即 在
在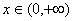 上为增函数
上为增函数
因此在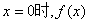 取得极小值
取得极小值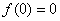 ,而且是最小值
,而且是最小值
于是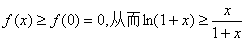 ,即
,即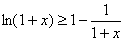
令 于是
于是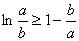 因此
因此
4、提示: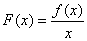 ,
,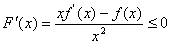 ,故
,故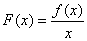 在(0,+∞)上是减函数,由
在(0,+∞)上是减函数,由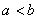 有
有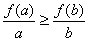
 af (b)≤bf (a) 故选(A)
af (b)≤bf (a) 故选(A)
-
导数常考题型总结
变化率与导数导数的运算考纲要求1导数概念及其几何意义1通过对大量实例的分析经历由平均变化率过渡到瞬时变化率的过程了解导数概念的实际…
-
导数题型归纳总结
导数题型归纳总结函数fx在x0处的导数fx0limx0fx0xfx0ylimxx0x函数yfx在点x0处的导数的几何意义是在该点处…
-
导数各类题型方法总结
导数各种题型方法总结请同学们高度重视首先关于二次函数的不等式恒成立的主要解法1分离变量2变更主元3根分布4判别式法5二次函数区间最…
-
强大 导数知识点各种题型归纳方法总结
导数的基础知识一导数的定义11函数yfx在xx0处的导数f39x0y39xxlimfx0xfx0xx02函数yfx的导数f39xy…
-
导数题型总结
导数及其应用题型总结题型一切线问题求曲线在点xoyo处的切线方程求过曲线外一点的切线方程求已知斜率的切线方程切线条数问题例题1已知…
-
强大 导数知识点各种题型归纳方法总结
导数的基础知识一导数的定义11函数yfx在xx0处的导数f39x0y39xxlimfx0xfx0xx02函数yfx的导数f39xy…
-
导数常考题型总结
变化率与导数导数的运算考纲要求1导数概念及其几何意义1通过对大量实例的分析经历由平均变化率过渡到瞬时变化率的过程了解导数概念的实际…
-
《导数及其应用》经典题型总结
导数及其应用经典题型总结一知识网络结构题型一求函数的导数及导数的几何意义考点一导数的概念物理意义的应用例11设函数fx在x2处可导…
-
导数题型总结
导数及其应用题型总结题型一切线问题求曲线在点xoyo处的切线方程求过曲线外一点的切线方程求已知斜率的切线方程切线条数问题例题1已知…
-
《导数各种题型及解法总结》---学生
导数各种题型及解法总结基础知识梳理第1页共9页胸中有了超越的目标就会充满激情学习就会充满动力生活就会充满活力1此类问题提倡按以下三…
-
导数题型归纳总结
导数题型归纳总结函数fx在x0处的导数fx0limx0fx0xfx0ylimxx0x函数yfx在点x0处的导数的几何意义是在该点处…