导数高考题型总结
高考题型总结(导数部分)
填空选择部分
1、已知函数y?f(x)的图象在点M(1,f(1))处的切线方程是y?
则f(1)?f?(1)? 。 1x?2, 2
4上,a为曲线在点P处的切线的倾斜角,则a的取值范围是( ) ex?1
????3?3?] (D) [,?) (A)[0,) (B)[,) (C) (,422444 123、 若函数f(x)?x?ax?lnx存在垂直于y轴的切线,则实数a的取值范围 22、已知点P在曲线y=
4
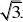
、设函数f(x)???)(0????),若f(x)?f?(x)为奇函数,则?=__________ 5、函数f(x)?xlnx?ax,(x?0)在[e,??)上递增,a的取值范围是6、 函数y=
A.(?1,1] 12x?㏑x的单调递减区间为( ) 2B.(0,1] C.[1,+∞) D.(0,+∞)
7、 已知f?x??ax3?3x2?x?1在R上是减函数,求a的取值范围8、设f(x)、g(x)是 R上的可导函数,f?(x) 、g?(x) 分别为f(x)、g(x)的导函数, 且满足条件f?(x)g(x)?f(x)g?(x)?0,则当a?x?b时,有 ( )
A.f(x)g(b)?f(b)g(x) B.f(x)g(a?)
C.f(x)g(x?) D.f(x)g(xf(b)g ( b?)f(a)g (xf(a)g (a
9、函数f(x)的定义域为R,f(?1)?2,对任意x?R,f?(x)?2,则f(x)?2x? 4的解集为( )
) D.(??,??) A.(?1,1) B.(?1,??) C.(??,?1
10、定义在(0,??)上的可导函数f(x)满足f'(x)?x?f(x)且f(2)?0则
f(x)?0的解集为( )x
A.(0,2) B.(0,2))(2,??) C.(2,??) D.?
211、已知函数f(x)?x?alnx.若函数g(x)?f(x)?2x在[1,4]上是减函数,求实数a的取值范围。
12、若函数f(x)=x(x-c)在x?2处有极大值,则常数c的值为_______;
13、设直线x?t与函数f(x)?x,g(x)?lnx的图像分别交于点M,N,则当|MN|达到最小时t的 值为( )
1 高考复习题(导数部分) 22
A.1 B.
14、设点P在曲线y?1 C
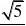
D
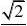
21x e上,点Q在曲线y?ln(2x)上,则|PQ|的最小值为( ) 2
(A)1?ln2 (B
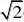
?ln2) (C)1?ln2 (D
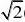
?ln2)
15、设f(x)?x?312x?2x?5,当x?[?1,2]时,f(x)?m恒成立,则实数m的取值范围2
为 。
16、已知P为曲线y?lnx上一点,则点P到直线y?x距离最小值为( )
A.1 B.2 2 C.2 D.2
解答题部分
1、设函数f(x)?ax2?bx?k(k?0)在x?0处取得极值,且曲线y?f(x)在点(1,f(1))处的切线垂直于直线x?2y?1?0.
⑴求a,b的值; ex
⑵若函数g(x)?,讨论g(x)的单调性. f(x)
2、已知函数f(x)?lnx?a,g(x)?f(x)?ax?6lnx,其中a?R . x
⑴讨论f(x)的单调性;
⑵若g(x)在其定义域内为增函数,求正实数a的取值范围;
3、设函数f(x)?1?a2x?ax?lnx(a?R). 2
2 高考复习题(导数部分)
⑴ 当a?1时,求函数f(x)的极值;
⑵当a?1时,讨论函数f(x)的单调性.
⑶若对任意a?(2,3)及任意x1,x2?[1,2],恒有ma?ln2?f(x1)?f(x2) 成立,求实数m的取值范围.
4、已知a?R,函数f(x)?(?x?ax)e2?x.(x?R,e为自然对数的底数)
⑴若函数f(x)在(?1,1)内单调递减,求a的取值范围;
⑵函数f(x)是否为R上的单调函数,若是,求出a的取值范围;若不是,请说明理由.
25、已知f(x)?6lnx?ax?8x?b (a,b为常数),且x?3是f(x)的一个极值点.
⑴求a的值;
⑵若y?f(x)的图象与x轴有且只有三个不同的交点,求b的取值范围.
6、已知
3 高考复习题(导数部分)
⑴求函数上的最小值; ⑵对一切恒成立,求实数的取值范围; ⑶证明:对一切
,都有成立.
高考真题
1、已知函数f(x)=ax?3x?1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围为( ) 32
A.(2,+∞) B.(-∞,-2) C.(1,+∞) D.(-∞,-1)
2、曲线y?e2x?1在点?0,2?处的切线与直线y?0和y?x围成的三角形的面积为( )
(A) 112 (B) (C) (D) 323
23、设f(x)?a(x?5)?6lnx,其中a?R,曲线y?f(x)在点(1,f(1))处的切线与y轴相较于
点(0,6).
⑴确定a的值;
⑵求函数f(x)的单调区间与极值.
4、设f(x)?alnx?
⑴ 求a的值;
⑵求函数f(x)的极值.
4 高考复习题(导数部分) 13?x?1,其中a?R,曲线y?f(x)在点(1,f(1))处的切线垂直于y轴. 2x2
bex?1
5、设函数f(x0?aelnx?,曲线y?f(x)在点(1,f(1)处的切线为y?e(x?1)?2. xx
⑴求a,b;
⑵证明:f(x)?1.
6、已知函数f(x)?ax?b在点(?1,f(?1))的切线方程为x?y?3?0. x2?1
⑴求函数f(x)的解析式;
⑵设g(x)?lnx,求证:g(x)?f(x)在x?[1,??)上恒成立.
7、已知函数f(x)?ae2x?be?2x?cx(a,b,c?R)的导函数f'(x)为偶函数,且曲线y?f(x)在点(0,f(0))处的切线的斜率为4?c.
⑴确定a,b的值;
⑵若c?3,判断
⑶若f(x)的单调性; f(x)有极值,求c的取值范围.
5 高考复习题(导数部分)
第二篇:高考导数问aa题常见题型总结
高考有关导数问题解题方法总结
一、考试内容
利用导数研究函数的单调性和极值,函数的最大值和最小值。
二、热点题型分析
题型一:利用导数几何意义求切线方程
1.曲线 在点
在点 处的切线方程是
处的切线方程是 
2.若曲线 在P点处的切线平行于直线
在P点处的切线平行于直线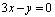 ,则P点的坐标为 (1,0)
,则P点的坐标为 (1,0)
3.若曲线 的一条切线
的一条切线 与直线
与直线 垂直,则
垂直,则 的方程为
的方程为 
4.求下列直线的方程:
(1)曲线 在P(-1,1)处的切线; (2)曲线
在P(-1,1)处的切线; (2)曲线 过点P(3,5)的切线;
过点P(3,5)的切线;
题型二:利用导数研究函数的极值、最值。
1.  在区间
在区间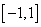 上的最大值是 2
上的最大值是 2
2.已知函数 处有极大值,则常数c= 6 ;
处有极大值,则常数c= 6 ;
3.函数 有极小值 -1 ,极大值 3
有极小值 -1 ,极大值 3
题型三:利用导数研究函数的单调性,极值、最值
2.已知三次函数 在
在 和
和 时取极值,且
时取极值,且 .
.
(1) 求函数 的表达式;
的表达式;
(2) 求函数 的单调区间和极值;
的单调区间和极值;
(3) 若函数 在区间
在区间 上的值域为
上的值域为 ,试求
,试求 、
、 应满足的条件.
应满足的条件.
3.设函数 .
.
(1)若 的图象与直线
的图象与直线 相切,切点横坐标为2,且
相切,切点横坐标为2,且 在
在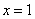 处取极值,求实数
处取极值,求实数 的值;
的值;
(2)当b=1时,试证明:不论a取何实数,函数 总有两个不同的极值点.
总有两个不同的极值点.
题型四:利用导数研究函数的图象
1 .如右图:是f(x)的导函数,
.如右图:是f(x)的导函数, 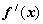 的图象如右图所示,则f(x)的图象只可能是( D )
的图象如右图所示,则f(x)的图象只可能是( D )
(A) (B) (C) (D)
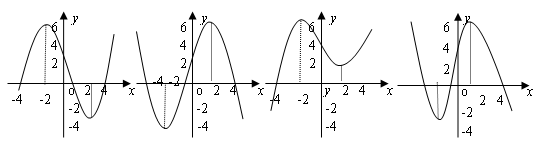
2.函数 ( A )
( A )
3.方程 ( B )
( B )
A、0 B、1 C、2 D、3
已知函数 的切线方程为y=3x+1
的切线方程为y=3x+1
(Ⅰ)若函数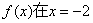 处有极值,求
处有极值,求 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,求函数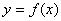 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(Ⅲ)若函数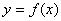 在区间[-2,1]上单调递增,求实数b的取值范围
在区间[-2,1]上单调递增,求实数b的取值范围
题型五:利用单调性、极值、最值情况,求参数取值范围
1.设函数
(1)求函数 的单调区间、极值.
的单调区间、极值.
(2)若当 时,恒有
时,恒有 ,试确定a的取值范围.
,试确定a的取值范围.
题型六:利用导数研究方程的根
1.已知平面向量 =(
=( ,-1).
,-1).  =(
=( ,
, ).
).
(1)若存在不同时为零的实数k和t,使 =
= +(t2-3)
+(t2-3) ,
, =-k
=-k +t
+t ,
, ⊥
⊥ ,
,
试求函数关系式k=f(t) ;
(2) 据(1)的结论,讨论关于t的方程f(t)-k=0的解的情况.
题型七:导数与不等式的综合
1.设 在
在 上是单调函数.
上是单调函数.
(1)求实数 的取值范围;
的取值范围;
(2)设 ≥1,
≥1, ≥1,且
≥1,且 ,求证:
,求证: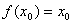 .
.
解:(1)  若
若 在
在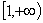 上是单调递减函数,则须
上是单调递减函数,则须 这样的实数a不存在.故
这样的实数a不存在.故 在
在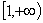 上不可能是单调递减函数.
上不可能是单调递减函数.
若 在
在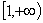 上是单调递增函数,则
上是单调递增函数,则 ≤
≤ ,
,
由于 .从而0<a≤3.
.从而0<a≤3.
(2)方法1、可知 在
在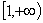 上只能为单调增函数. 若1≤
上只能为单调增函数. 若1≤ ,则
,则 若1≤
若1≤ 矛盾,故只有
矛盾,故只有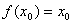 成立.
成立.
方法2:设 ,
, 两式相减得
两式相减得
 ≥1,u≥1,
≥1,u≥1,
 ,
,
2.已知 为实数,函数
为实数,函数
(1)若函数 的图象上有与
的图象上有与 轴平行的切线,求
轴平行的切线,求 的取值范围
的取值范围
(2)若 ,(Ⅰ)求函数
,(Ⅰ)求函数 的单调区间
的单调区间
(Ⅱ)证明对任意的 ,不等式
,不等式 恒成立
恒成立
解: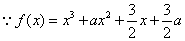 ,
,
 函数
函数 的图象有与
的图象有与 轴平行的切线,
轴平行的切线, 有实数解
有实数解
 ,
, ,所以
,所以 的取值范围是
的取值范围是
 ,
, ,
, ,
,
由 或
或 ;由
;由
 的单调递增区间是
的单调递增区间是 ;单调减区间为
;单调减区间为
易知 的最大值为
的最大值为 ,
, 的极小值为
的极小值为 ,又
,又
 在
在 上的最大值
上的最大值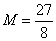 ,最小值
,最小值
 对任意
对任意 ,恒有
,恒有
题型八:导数在实际中的应用
 1.请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心
1.请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
解:设OO1为
 ,则
,则
由题设可得正六棱锥底面边长为: ,(单位:
,(单位: )
)
故底面正六边形的面积为:
 =
= ,(单位:
,(单位: )
)
帐篷的体积为:

 (单位:
(单位: )
)
求导得 。
。
令 ,解得
,解得 (不合题意,舍去),
(不合题意,舍去), ,
,
当 时,
时, ,
, 为增函数;
为增函数;
当 时,
时, ,
, 为减函数。
为减函数。
∴当 时,
时, 最大。
最大。
答:当OO1为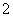
 时,帐篷的体积最大,最大体积为
时,帐篷的体积最大,最大体积为
 。
。
2.统计表明,某种型号的汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
解:(I)当 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了 小时,
小时,
要耗没 (升)。
(升)。
(II)当速度为 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了 小时,设耗油量为
小时,设耗油量为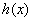 升,
升,
依题意得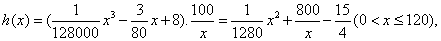

令 得
得
当 时,
时,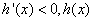 是减函数;
是减函数;
当 时,
时, 是增函数。
是增函数。
 当
当 时,
时,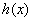 取到极小值
取到极小值
因为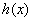 在
在 上只有一个极值,所以它是最小值。
上只有一个极值,所以它是最小值。
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升。
题型九:导数与向量的结合
1.设平面向量 若存在不同时为零的两个实数s、t及实数k,使
若存在不同时为零的两个实数s、t及实数k,使
(1)求函数关系式 ;
;
(2)若函数 在
在 上是单调函数,求k的取值范围。
上是单调函数,求k的取值范围。
解:(1)


(2)

则在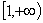 上有
上有
由 ;
;
由 。
。
因为在t∈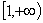 上
上 是增函数,所以不存在k,使
是增函数,所以不存在k,使 在
在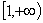 上恒成立。故k的取值范围是
上恒成立。故k的取值范围是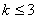 。
。
-
导数常考题型总结
变化率与导数导数的运算考纲要求1导数概念及其几何意义1通过对大量实例的分析经历由平均变化率过渡到瞬时变化率的过程了解导数概念的实际…
-
导数题型归纳总结
导数题型归纳总结函数fx在x0处的导数fx0limx0fx0xfx0ylimxx0x函数yfx在点x0处的导数的几何意义是在该点处…
-
导数各类题型方法总结
导数各种题型方法总结请同学们高度重视首先关于二次函数的不等式恒成立的主要解法1分离变量2变更主元3根分布4判别式法5二次函数区间最…
-
强大 导数知识点各种题型归纳方法总结
导数的基础知识一导数的定义11函数yfx在xx0处的导数f39x0y39xxlimfx0xfx0xx02函数yfx的导数f39xy…
-
导数题型总结
导数及其应用题型总结题型一切线问题求曲线在点xoyo处的切线方程求过曲线外一点的切线方程求已知斜率的切线方程切线条数问题例题1已知…
-
强大 导数知识点各种题型归纳方法总结
导数的基础知识一导数的定义11函数yfx在xx0处的导数f39x0y39xxlimfx0xfx0xx02函数yfx的导数f39xy…
-
导数常考题型总结
变化率与导数导数的运算考纲要求1导数概念及其几何意义1通过对大量实例的分析经历由平均变化率过渡到瞬时变化率的过程了解导数概念的实际…
-
《导数及其应用》经典题型总结
导数及其应用经典题型总结一知识网络结构题型一求函数的导数及导数的几何意义考点一导数的概念物理意义的应用例11设函数fx在x2处可导…
-
导数题型总结
导数及其应用题型总结题型一切线问题求曲线在点xoyo处的切线方程求过曲线外一点的切线方程求已知斜率的切线方程切线条数问题例题1已知…
-
《导数各种题型及解法总结》---学生
导数各种题型及解法总结基础知识梳理第1页共9页胸中有了超越的目标就会充满激情学习就会充满动力生活就会充满活力1此类问题提倡按以下三…
-
导数题型归纳总结
导数题型归纳总结函数fx在x0处的导数fx0limx0fx0xfx0ylimxx0x函数yfx在点x0处的导数的几何意义是在该点处…