浅谈数学归纳法
浅谈“数学归纳法”
论文摘要:“观察—归纳—猜想—论证”的思想方法,既能发现问题,又能证明结论,还能激发学习兴趣,它是由揭露个别事物或某一对象的部分属性过渡到一般或整体的思维形式。由于归纳推理的过程和人类认识进程的一致性,因而这种推理方法显得非常自然,容易被人接受,是认识数学真理的一个重要手段,其地位越来越重要,数学归纳法正是应用这一思想方法来证明某些与自然数n有关的数学命题的一种方法。本文简单总结了一下它的基本依据和证明过程,以及它两个条件的内在联系,然后回顾了一下数学归纳法的各种其他形式,在原来的基础上拓宽了对数学归纳法的认识。最后举例说明数学归纳法的应用,其中有代数、不等式方面的证明,也有几何方面的典型例子,从中可以窥见数学归纳法的强大功能。
正文:
已知最早的使用数学归纳法的证明出现于Francesco Maurolico的Arithmeticorum libri duo(1575年)。Maurolico利用递推关系巧妙的证明出证明了前n个奇数的总和是n^2,由此揭开了数学归纳法之谜。最简单和常见的数学归纳法证明方法是证明当n属于所有正整数时一个表达式成立,这种方法是由下面两步组成:
(1)递推的基础:证明当n=1时表达式成立。
(2)递推的依据:证明如果当n=m时成立,那么当n=m+1时同样成立。
这种方法的原理在于第一步证明起始值在表达式中是成立的,然后证明一个值到下一个值的证明过程是有效的。如果这两步都被证明了,那么任何一个值的证明都可以被包含在重复不断进行的过程中。或许想成多米诺效应更容易理解一些,如果你有一排很长的直立着的多米诺骨牌那么如果你可以确定:第一张骨牌将要倒下,只要某一个骨牌倒了,与之相邻的下一个骨牌也要倒,那么你就可以推断所有的的骨牌都将要倒。这样就确定出一种递推关系,只要满足两个条件就会导致所有骨牌全都倒下:(1)第一块骨牌倒下;(2)任意两块相邻骨牌,只要前一块倒下,后一块必定倒下。这样,无论有多少骨牌,只要保证(1)(2)成立,就会全都倒下。
一.数学归纳法(证明某些与正整数 有关的命题时常常采用的方法)证明命题的步骤:
有关的命题时常常采用的方法)证明命题的步骤:
(1)(归纳奠基)证明当 取第一个值
取第一个值 时命题成立;
时命题成立;
(2)(归纳递推)假设当 时命题成立,证明当
时命题成立,证明当 时命题也成立;
时命题也成立;
根据(1)和(2),可知命题对于从 开始的所有正整数
开始的所有正整数 都成立.
都成立.
应用类比的方法,类比多米诺骨牌游戏和数学归纳法,在多米诺骨牌游戏过程中,体会所有骨牌都倒下,第1块骨牌必须倒下,这是基础,也是前提条件.在多米诺骨牌游戏过程中,第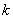 块骨牌不能拿走,因为第
块骨牌不能拿走,因为第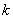 块骨牌的存在,是所有骨牌都倒下的保证,这就是多米诺骨牌游戏的连续性.
块骨牌的存在,是所有骨牌都倒下的保证,这就是多米诺骨牌游戏的连续性.
分析:根据“第一块骨牌倒下”抽象出数学归纳法的第一步,即(1)(归纳奠基)证明当 取第一个值
取第一个值 (
(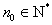 ,例如
,例如 =1或
=1或 )时,命题成立.
)时,命题成立.
根据“任意相邻的两块骨牌,前一块倒下一定导致后一块倒下”,抽象出数学归纳法的第二步,即(2)(归纳递推)假设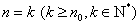 时命题成立,证明当
时命题成立,证明当 时命题也成立.
时命题也成立.
从完成“多米诺骨牌游戏”中,抽象出数学归纳法证明命题的结论,即由(1),(2)可知,命题对于从 开始的所有正整数
开始的所有正整数 都成立.
都成立.
通过对多米诺骨牌游戏的分析,让我们了解了从具体到抽象的归纳和概括过程,从而理解数学归纳法的本质.
体会并理解“归纳奠基”和“归纳递推”,知道只有把“归纳奠基”与“归纳递推”结合起来,才能完成数学归纳法的证明过程,理解数学归纳法的证明步骤.
二.数学归纳法与其他数学方法的区别:
“数学归纳法”它可以完成通过有限个步骤的推理,证明 取所有正整数都成立的命题的证明.例如,在高中阶段,在等差数列和等比数列知识的学习过程中,我们用不完全归纳法推出了它们的通项公式,然而其中正确性的严格证明则需要用数学归纳法进行.
取所有正整数都成立的命题的证明.例如,在高中阶段,在等差数列和等比数列知识的学习过程中,我们用不完全归纳法推出了它们的通项公式,然而其中正确性的严格证明则需要用数学归纳法进行.
归纳法和演绎法都是重要的数学方法,归纳法中的完全归纳法和演绎法都是逻辑方法;不完全归纳法是非逻辑方法,只是用于数学发现规律,不是用于数学严谨证明。
数学归纳法不是演绎法,而是一种递归推理。它是在可靠的基础上,利用命题自身具有的传递性,运用“有限”的手段,来解决“无限”的问题.它克服了完全归纳法的繁杂、不可行的缺点,又克服了不完全归纳法结论不可靠的不足,使我们认识到事情由简到繁、由特殊到一般、由有限到无穷.其蕴含的数学思想方法有归纳的思想,递推的思想,特殊到一般的思想,有限到无限的思想方法.
三.数学归纳法的基本理论依据:
数学归纳法的原理,通常被规定作为自然数公理。数学归纳法证明的是与自然数有关的命题,它的依据是皮亚诺提出的自然数的序数理论,就是通常所说的自然数的皮亚诺公理,内容是:设 是正整数的一个子集,且它具有下列性质:①
是正整数的一个子集,且它具有下列性质:① ;②若
;②若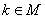 ,则
,则 .那么
.那么 是全体正整数的集合,即
是全体正整数的集合,即 )也叫做归纳公理.设
)也叫做归纳公理.设 是一个与正整数有关的命题,我们把使
是一个与正整数有关的命题,我们把使 成立的所有正整数组成的集合记为
成立的所有正整数组成的集合记为 ,如果要证明
,如果要证明 对于所有正整数都成立,只要证明
对于所有正整数都成立,只要证明 即可.为此,根据归纳公理,首先证明
即可.为此,根据归纳公理,首先证明 (数学归纳法中的第一步“归纳奠基”正是进行这样的证明);其次证明若
(数学归纳法中的第一步“归纳奠基”正是进行这样的证明);其次证明若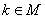 ,则
,则 (数学归纳法中的第二步“归纳递推”正是进行这样的证明).这样即可得到
(数学归纳法中的第二步“归纳递推”正是进行这样的证明).这样即可得到 ,从而证明了命题
,从而证明了命题 对于一切正整数都成立.不难看出归纳公理是数学归纳法的理论根据,数学归纳法的两个证明步骤恰是验证这条公理所说的两个性质.
对于一切正整数都成立.不难看出归纳公理是数学归纳法的理论根据,数学归纳法的两个证明步骤恰是验证这条公理所说的两个性质.
四.数学归纳法的基本思想:
即先验证使结论有意义的最小的正整数 ,如果当
,如果当 时,命题成立,再假设当
时,命题成立,再假设当 时命题成立,利用这个假设,如果能推出当
时命题成立,利用这个假设,如果能推出当 时,命题也成立,那么就可以递推出对所有的正整数
时,命题也成立,那么就可以递推出对所有的正整数 ,
, ………,命题都成立.也就是说,当
………,命题都成立.也就是说,当 时命题成立,可以推出
时命题成立,可以推出 时命题成立,当
时命题成立,当 时命题成立,可以推出
时命题成立,可以推出 时命题成立,…….即命题
时命题成立,…….即命题 真
真 命题
命题 真
真 命题
命题 真
真 命题
命题 真
真 .因此可知命题对于从
.因此可知命题对于从 开始的所有正整数
开始的所有正整数 都成立.
都成立.
五.数学归纳法的思维模式是:“观察——归纳——猜想——论证”.
数学归纳法教学的重点是借助具体实例了解数学归纳法的基本思想,掌握它的基本步骤,运用它证明一些与正整数 (
( 取无限多个值)有关的数学命题.
取无限多个值)有关的数学命题.
数学归纳法的适用范围仅限于与正整数有关的命题,在证明过程中,要分“两个步骤和一个结论”.其中第一步是归纳奠基,只需验证 取第一个值
取第一个值 (这里
(这里 是使结论有意义的最小的正整数,它不一定是1,可以是2,或取别的正整数)时命题成立;第二步是归纳递推,就是要证明命题的传递性.把第一步的结论和第二步的结论联系起来,才可以断定命题对所有的正整数都成立.因此,用数学归纳法证明命题时,完成了上述两个步骤后,还应该有一个总的结论.否则,还不能算是已经证明完毕.所以,严格地说,用数学归纳法证明命题的完整过程应该是“两个步骤和一个结论”.缺了第(1)步,就没有了归纳奠基;缺了第(2)步,就丧失了归纳递推的过程;缺了结论,整个数学归纳法的过程就不能顺利完成.“两个步骤和一个结论”缺一不可。
是使结论有意义的最小的正整数,它不一定是1,可以是2,或取别的正整数)时命题成立;第二步是归纳递推,就是要证明命题的传递性.把第一步的结论和第二步的结论联系起来,才可以断定命题对所有的正整数都成立.因此,用数学归纳法证明命题时,完成了上述两个步骤后,还应该有一个总的结论.否则,还不能算是已经证明完毕.所以,严格地说,用数学归纳法证明命题的完整过程应该是“两个步骤和一个结论”.缺了第(1)步,就没有了归纳奠基;缺了第(2)步,就丧失了归纳递推的过程;缺了结论,整个数学归纳法的过程就不能顺利完成.“两个步骤和一个结论”缺一不可。
六.数学归纳法的表现形式:
(一)第一数学归纳法:一般地,证明一个与自然数n有关的命题P(n),有如下步骤:
(1)证明当n取第一个值n0时命题成立。n0对于一般数列取值为0或1,但也有特殊情况;
(2)假设当n=k(k≥n0,k为自然数)时命题成立,证明当n=k+1时命题也成立。
综合(1)(2),对一切自然数n(≥n0),命题P(n)都成立。
(二)第二数学归纳法: 对于某个与自然数有关的命题P(n),
(1)验证n=n0时P(n)成立;
(2)假设n0≤n<k时P(n)成立,并在此基础上,推出P(k+1)成立。
综合(1)(2),对一切自然数n(≥n0),命题P(n)都成立。
(三)倒推归纳法(反向归纳法):
(1)验证对于无穷多个自然数n命题P(n)成立(无穷多个自然数可以是一个无穷数列中的数,如对于算术几何不等式的证明,可以是2^k,k≥1);
(2)假设P(k+1)(k≥n0)成立,并在此基础上,推出P(k)成立,
综合(1)(2),对一切自然数n(≥n0),命题P(n)都成立;
(四)螺旋式归纳法 对两个与自然数有关的命题P(n),Q(n),
(1)验证n=n0时P(n)成立;
(2)假设P(k)(k>n0)成立,能推出Q(k)成立,假设 Q(k)成立,能推出 P(k+1)成立;
综合(1)(2),对一切自然数n(≥n0),P(n),Q(n)都成立。
数学归纳法还有几种其他表现形式:
(一)简单归纳法。即在归纳步中,归纳假设为“n=k 时待证命题成立”。
这是最常用的一种归纳法,称为简单归纳法,大家都比较熟悉,这里不再赘述。
(二)广义归纳法。数学归纳法不仅可用于含有自然数变元n 的命题,经推广后,还可用于含有某些其它集合上的命题。这种集合,称为归纳集。对于一个含有某个归纳集上的变元x 的待证命题P(x),所用的归纳法称之为广义归纳法。
定义:设有一个集合A,如果它满足下面三个性质:
(1)a1,a2?,an 是A 中的元素(n≥1);
(2)如果x 是A 中元素,则f11(x),f12(x),?f1n1(x)也是A 中的元素(n、>0);
如果x,y 是A 是元素,则f21(x、y),f22(x,y),?f2n2(x,y)也是A 中元素(n2>0);?;如果x1?,xm 是A 中元素,则fm1 xl?xm),fm2(xl?,xm),?fmnm(x1?,xm)也是A 中元素(m≥l,nm>0)。
(3)A 中的元素仅限于此。
则A 称之为归纳集a1,a2,?an 称为该集的开始元素,诸fij 称为该集
的生成函数(其中第一下标为该函数的元素,第二下标以区分具有同样元素
的各函数)。
按照上述的定义,自然数集是归纳集,它的开始元素是0,生成函数是f(x)=x+1。
前例中集{a,b,c,d}的元素利用“+”,“-”运算所构成的一切表
达式的集合是归纳集,开始元素是是a,b,c,d,生成函数为f21(x,y)=x+y,f22(x,y)=x-y。
在证明含有某个归纳集A 上的变元X 的待证命题P(x)时,可用如下的广义归纳法。
奠基步要证明(al),P(a2),??P(an)成立,这里 al,a2?,an是 A 中的开始元素。
归纳法要证明对于 1≤i≤m 及1≤j≤n 的所有 i、j 对于 A 中的任何元素x1,x2?,xi,如果P(xl),P(x2),?,P(x1)成立,则P(fij(xx1,?,xi))也成立。在例 4 中,因为表达式所组成的集合是归纳集(记为 A),我们可用广义归纳法证之。
奠基:对于A 中的四个开始元素a,b,C,d,因为它们的标识符个数为1, 而运算符个数均为0,所以命题成立。归纳:对于A 中的元素x,y,f21(x,y)=x+y 中,我们设x+y 标识符个数为m,运算符个数为n;x 中标识符个数为ml,运算符个数为nl;x 中标识符个数为m2,运算符个数为n2;则m=ml+m2=(n1+1)+(n2+1)(nl+n+1)+1=n+1.同理可证f22(x,y)=x-y 也有如上的结果,故依广义归纳法,本命题成立。
七.数学归纳法的应用:
(1)确定一个表达式在所有自然数范围内是成立的或者用于确定一个其他的形式在一个无穷序列是成立的。
(2)数理逻辑和计算机科学广义的形式的观点指出能被求出值的表达式是等价表达式。
(3)证明数列前n项和与通项公式的成立。
(4)证明和自然数有关的不等式。
只针对偶数或只针对奇数:
如果我们想证明的命题并不是针对全部自然数,而只是针对所有奇数或偶数,那么证明的步骤需要做如下修改:
奇数方面:第一步,证明当n=1时命题成立。 第二步,证明如果n=m成立,那么可以推导出n=m+2也成立。
偶数方面:第一步,证明当n=0或2时命题成立。 第二步,证明如果n=m成立,那么可以推导出n=m+2也成立。
递降归纳法:数学归纳法并不是只能应用于形如“对任意的n”这样的命题。对于形如“对任意的n=0,1,2,...,m”这样的命题,如果对一般的n比较复杂,而n=m比较容易验证,并且我们可以实现从k到k-1的递推,k=1,...,m的话,我们就能应用归纳法得到对于任意的n=0,1,2,...,m,原命题均成立。
八.有关数学归纳法的例题:
例1.用数学归纳法证明:
 .
.
请读者分析下面的证法:
证明:①n=1时,左边 ,右边
,右边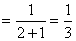 ,左边=右边,等式成立.
,左边=右边,等式成立.
②假设n=k时,等式成立,即:
 .
.
那么当n=k+1时,有:




这就是说,当n=k+1时,等式亦成立.
由①、②可知,对一切自然数n等式成立.
评述:上面用数学归纳法进行证明的方法是错误的,这是一种假证,假就假在没有利用归纳假设n=k这一步,当n=k+1时,而是用拆项法推出来的,这样归纳假设起到作用,不符合数学归纳法的要求.
正确方法是:当n=k+1时.




这就说明,当n=k+1时,等式亦成立,
例2.是否存在一个等差数列{an},使得对任何自然数n,等式:a1+2a2+3a3+…+nan=n(n+1)(n+2)都成立,并证明你的结论.
分析:采用由特殊到一般的思维方法,先令n=1,2,3时找出来{an},然后再证明一般性.
解:将n=1,2,3分别代入等式得方程组.
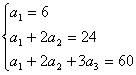 ,
,
解得a1=6,a2=9,a3=12,则d=3.
故存在一个等差数列an=3n+3,当n=1,2,3时,已知等式成立.
下面用数学归纳法证明存在一个等差数列an=3n+3,对大于3的自然数,等式
a1+2a2+3a3+…+nan=n(n+1)(n+2)都成立.
因为起始值已证,可证第二步骤.
假设n=k时,等式成立,即a1+2a2+3a3+…+kak=k(k+1)(k+2)
那么当n=k+1时,
a1+2a2+3a3+…+kak +(k+1)ak+1
= k(k+1)(k+2)+ (k+1)[3(k+1)+3]
=(k+1)(k2+2k+3k+6)
=(k+1)(k+2)(k+3)
=(k+1)[(k+1)+1][(k+1)+2]
这就是说,当n=k+1时,也存在一个等差数列an=3n+3使a1+2a2+3a3+…+nan=n(n+1)(n+2)成立.
综合上述,可知存在一个等差数列an=3n+3,对任何自然数n,等式a1+2a2+3a3+…+nan=n(n+1)(n+2)都成立.
例3.证明不等式 (n∈N).
(n∈N).
证明:①当n=1时,左边=1,右边=2.
左边<右边,不等式成立.
②假设n=k时,不等式成立,即 .
.
那么当n=k+1时,



这就是说,当n=k+1时,不等式成立.
由①、②可知,原不等式对任意自然数n都成立.
说明:这里要注意,当n=k+1时,要证的目标是
 ,当代入归纳假设后,就是要证明:
,当代入归纳假设后,就是要证明:
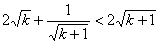 .
.
认识了这个目标,于是就可朝这个目标证下去,并进行有关的变形,达到这个目标.
例4.已知数列{an}满足a1=0,a2=1,当n∈N时,an+2=an+1+an.
求证:数列{an}的第4m+1项(m∈N)能被3整除.
分析:本题由an+1=an+1+an求出通项公式是比较困难的,因此可考虑用数学归纳法.
①当m=1时,a4m+1=a5=a4+a3=(a3+a2)+(a2+a1)=a2+a1+a2+a2+a1=3,能被3整除.
②当m=k时,a4k+1能被3整除,那么当n=k+1时,
a4(k+1)+1=a4k+5=a4k+4+a4k+3
=a4k+3+a4k+2+a4k+2+a4k+1
=a4k+2+a4k+1+a4k+2+a4k+2+a4k+1
=3a4k+2+2a4k+1
由假设a4k+1能被3整除,又3a4k+2能被3整除,故3a4k+2+2a4k+1能被3整除.
因此,当m=k+1时,a4(k+1)+1也能被3整除.
由①、②可知,对一切自然数m∈N,数列{an}中的第4m+1项都能被3整除.
例5.n个半圆的圆心在同一条直线l上,这n个半圆每两个都相交,且都在直线l的同侧,问这些半圆被所有的交点最多分成多少段圆弧?
分析:设这些半圆最多互相分成f (n)段圆弧,采用由特殊到一般的方法,进行猜想和论证.



当n=2时,由图(1).两个半圆交于一点,则分成4段圆弧,故f (2)=4=22.
当n=3时,由图(2).三个半径交于三点,则分成9段圆弧,故f (3)=9=32.
由n=4时,由图(3).三个半圆交于6点,则分成16段圆弧,故f (4)=16=42.
由此猜想满足条件的n个半圆互相分成圆弧段有f (n)=n2.
用数学归纳法证明如下:
①当n=2时,上面已证.
②设n=k时,f (k)=k2,那么当n=k+1时,第k+1个半圆与原k个半圆均相交,为获得最多圆弧,任意三个半圆不能交于一点,所以第k+1个半圆把原k个半圆中的每一个半圆中的一段弧分成两段弧,这样就多出k条圆弧;另外原k个半圆把第k+1个半圆分成k+1段,这样又多出了k+1段圆弧.
∴ f (k+1)=k2+k+(k+1)
=k2+2k+1=(k+1)2
∴ 满足条件的k+1个半圆被所有的交点最多分成(k+1)2段圆弧.
由①、②可知,满足条件的n个半圆被所有的交点最多分成n2段圆弧.
说明:这里要注意;增加一个半圆时,圆弧段增加了多少条?可以从f (2)=4,f (3)=f (2)+2+3,f (4)=f (3)+3+4中发现规律:f (k+1)=f (k)+k+(k+1).
九.参考文献:
(1)华罗庚 .数学归纳法 [M] 北京:科学出版社,2002. 12-15
(2)王力,张宇.数学归纳法的教学[J].初等数学研究.2007, 23(9).120-123
(3)G 波 利 亚 著 . 涂 泓 , 冯 承 天 译 . 怎 样 解 题 [M]. 上 海 : 上 海 科 技 教 育 出 版 社
(4)张鹏志.高中代数解题方法汇集 [M] 青岛出版社第一版.1992,228-238
(5)张雄,李得虎.数学方法论与解题研究 [M] 高等教育出版社第一版,2003,49-62
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
新课标高二数学归纳法(经典总结)
数学归纳法极限一第一数学归纳法一般地证明一个与自然数n有关的命题Pn有如下步骤1证明当n取第一个值n0时命题成立n0对于一般数列取…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
理科数学归纳法知识总结
理科数学归纳法知识总结一基本概念1运用数学归纳法证明命题要分两步第一步是归纳奠基或递推基础第二步是归纳递推或归纳假设两步缺一不可二…
-
数学归纳法教案(新)
教材背景:归纳是一种由特殊事例导出一般规律的思维方法.归纳推理分完全归纳推理与不完全归纳推理两种.不完全归纳推理只根据一类事物中的…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…