数列专题复习(全是精华)

一、证明等差等比数列

1． 等差数列的证明方法：

 （1）定义法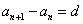：(常数)   （2）等差中项法：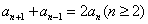

2．等比数列的证明方法：

（1）定义法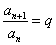：(常数)  （2）等比中项法：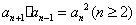                    

例1.设｛a_n｝为等差数列，S_n为数列｛a_n｝的前n项和，已知S₇＝7，S₁₅＝75，

T_n为数列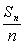｛｝的前n项和，求T_n．

解：设等差数列｛a_n｝的公差为d，则

S_n=na₁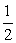＋n（n－1）d．∴S₇＝7，S₁₅＝75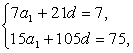，∴即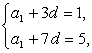

解得a₁＝－2，d＝1．∴＝a₁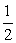＋（n－1）d＝－2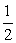＋（n－1）．

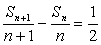∵，∴数列｛｝是等差数列，其首项为－2，公差为，

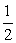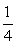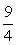∴T_n＝n²－n．

例2．设数列{a_n}的首项a₁=1，前n项和S_n满足关系式：

3tS_n－（2t+3）S_n－1=3t（t>0，n=2，3，4，…）

求证：数列{a_n}是等比数列；

解：（1）由a₁=S₁=1，S₂=1+a₂，得a₂=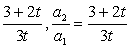

又3tS_n－（2t+3）S_n－1=3t           ①

3tS_n－1－（2t+3）S_n－2=3t    ②

①－②得3ta_n－（2t+3）a_n－1=0 ∴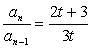，（n=2，3，…）

所以{a_n}是一个首项为1，公比为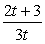的等比数列.

练习：已知a₁=2，点(a_n,a_n+1)在函数f(x)=x²+2x的图象上，其中=1，2，3，…

（1）       证明数列｛lg(1+a_n)｝是等比数列；

（2）       设T_n=(1+a₁) (1+a₂) …(1+a_n)，求T_n及数列｛a_n｝的通项；

答案 .(2) ,;

二．通项的求法

（1）利用等差等比的通项公式

(2)累加法：

例3．已知数列满足，，求。

解：由条件知：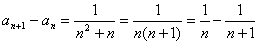

分别令，代入上式得个等式累加之，即

所以

，

（3）构造等差或等比或

例4．已知数列满足

       求数列的通项公式；

解：

      

       是以为首项，2为公比的等比数列。

      

       即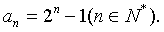　

例5．已知数列中，,，求.

解：在两边乘以得：

令，则,解之得：,所以.

练习:已知数列满足，且。

       （1）求；  （2）求数列的通项公式。

解：       （1）

       （2）

             

       ∴    

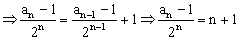
（4）利用

例6．若和分别表示数列和的前项和，对任意正整数

，.求数列的通项公式；

解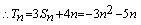： ……2分  当

  当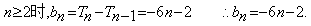……4分

练习：1. 已知正项数列{a_n}，其前n项和S_n满足10S_n=a_n²+5a_n+6且a₁,a₃,a₁₅成等比数列，求数列{a_n}的通项a_n  

解: ∵10S_n=a_n²+5a_n+6， ①   ∴10a₁=a₁²+5a₁+6，解之得a₁=2或a₁=3  

又10S_n－1=a_n－1²+5a_n－1+6(n≥2)，②

 由①－②得 10a_n=(a_n²－a_n－1²)+6(a_n－a_n－1)，即(a_n+a_n－1)(a_n－a_n－1－5)=0 

∵a_n+a_n－1>0  ， ∴a_n－a_n－1=5 (n≥2)  

当a₁=3时，a₃=13，a₁₅=73   a₁， a₃，a₁₅不成等比数列∴a₁≠3;

当a₁=2时， a₃=12， a₁₅=72， 有 a₃²=a₁a₁₅ ， ∴a₁=2， ∴a_n=5n－3 

2．设数列的前项的和

，

（Ⅰ）求首项与通项；

（Ⅱ）设，，证明：

解：（I），解得：

所以数列是公比为4的等比数列

所以：

得：  （其中n为正整数）

（II）

所以：

 

 

（5）累积法    转化为，逐商相乘.

例7．已知数列满足，，求。

解：由条件知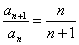，分别令，代入上式得个等式累乘之，即

又，

练习：1.已知， ，求。

解：  。

2．已知数列{a_n}，满足a₁=1， (n≥2)，

则{a_n}的通项  

解：由已知，得，用此式减去已知式，得

当时，，即，又，

，将以上n个式子相乘，得

（6）倒数变形：,两边取倒数后换元转化为。

例8：已知数列｛a_n｝满足：，求数列｛a_n｝的通项公式。

解：取倒数：

是等差数列，

练习：已知数列｛a_n｝满足：a₁＝，且a_n＝

求数列｛a_n｝的通项公式；

解：将条件变为：1－＝，因此｛1－｝为一个等比数列，其首项为

1－＝，公比，从而1－＝，据此得a_n＝（n³1）

三．数列求和

1、等差数列求和公式：  

2、等比数列求和公式：

3、错位相减法求和

{ a_n }、{ b_n }分别是等差数列和等比数列.

例9． 求和：

解：由题可知，设………………………①

…②（设制错位）

①－②得     （错位相减）再利用等比数列的求和公式得：。

∴   

练习： 求数列前n项的和.

解：由题可知，{}的通项是等差数列{2n}的通项与等比数列{}的通项之积

设…………………………………①

…………② ①－②得 

∴  

4、倒序相加法求和

这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个.

5、分组法求和

有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.

例10． 求数列的前n项和：，…

解：设

将其每一项拆开再重新组合得

（分组）

当a＝1时，＝（分组求和）

当时，＝

6、裂项法求和

这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的. 通项分解（裂项）

（1）为等差数列，

（2）

例11． 求数列的前n项和.

解：设，则                                       

＝

例12．  在数列{a_n}中，，又，求数列{b_n}的前n项的和.

解： 　 ∵

    　 ∴  数列{b_n}的前n项和：

 ＝ ＝

练习：

1．已知数列{}的前项和为，且满足 。求数列{}的通项公式；

解：（1）数列{}的前项和为，且满足

则    （）

相减得：       （）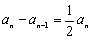 

又当n=1时，， ，

{}是以为首项，公比的等比数列

     （）

2．已知数列：

①求证数列为等差数列，并求它的公差

②设，求。

解：①由条件，

∴；∴

故为等差数列，公差

②

又知

∴

 

第二篇：高三_数列专题(精华

高三 数列专题1

1.已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}．．

满足bn?1，其前n项和为Sn． an?an?1

（1）求数列{an}的通项公式an；

（2）若S2为S1，Sm(m∈N*)的等比中项，求m的值．

?a?3?a1?2d,35解：（1）由题意，得?1解得< d <． ?????????3分 22?a1?d?5?a1?3d,

又d∈Z，∴d = 2．∴an=1+(n－1)?2=2n－1． ?????????6分

（2）∵bn?11111??(?)， an?an?1(2n?1)(2n?1)22n?12n?1

11n111111∴Sn?[(1?)?(?)?????(．11分 )??)]?(1?22n?12n?123352n?12n?1

∵S1?2

212m，S2?，Sm?，S2为S1，Sm(m∈N?)的等比中项， 352m?12m?2?1∴S?SmS1，即????， ?????????14分 ?5?32m?1

解得m=12． ?????????15分

2.数列{an}的前n项和记为Sn，a1?t，an?1?2Sn?1(n?N?)．

（1）当t为何值时，数列{an}是等比数列？

（2）在（1）的条件下，若等差数列{bn}的前n项和Tn有最大值，且T3?15，又a1?b1, a2?b2,a3?b3成等比数列，求Tn．

【解】（1）由an?1?2Sn?1，可得an?1?2Sn?1?1(n?2)，

两式相减得an?1?an?2an,即an?1?3an(n?2)，

∴当n?2时，{an}是等比数列， ???????????????????3分 要使n?1时，{an}是等比数列，则只需

（2）设{bn}的公差为d， a22t?1??3，从而t?1． ??6分 a1t

1

由T3?15得b1?b2?b3?15，于是b2?5， ?????????????8分 故可设b1?5?d,b3?5?d，

又a1?1,a2?3,a3?9，

由题意可得(5?d?1)(5?d?9)?(5?3)2，解得d1?2,d2??10， ∵等差数列{bn}的前n项和Tn有最大值，

∴d?0,d??10， ??????????????????????10分 n(n?1)?(?10)?20n?5n2． ????????????12分 2

a(1?an). 4.已知数列{an}满足a1?a(a?0,且a?1),前n项和为Sn,且Sn?1?a∴Tn?15n?

（I）求证：{an}是等比数列；

（II）记bn?anlg|an|(n?N*),当a??7时，是否存在正整数m，使得对于任意正3

整数n，都有bn?bm？如果存在，求出m的值；如果不存在，说明理由。

【解】当n?2时,Sn?

?an?Sn?Sn?1aa(1?an),Sn?1?(1?an?1)， 1?a1?aaa?[(1?an)?(1?an?1)]?(an?1?an)， ????3分 1?a1?a

即an?aan?1.又a1?a?0， ????5分

所以，{an}是首项和公比都为a的等比数列。 ????6分

（II）解：由（I）知，an?an,bn?anlg|an|?nanlg|a|. ????7分

7?(?1,0),则lg|a|?0. 3

所以,当n为偶数时,bn?nanlg|a|?0;n为奇数时,bn?0.又a??

可见，若存在满足条件的正整数m，则m为偶数。 ????9分

2

b2k?2?b2k?[(2k?2)a2k?2?2ka2k]lg|a|

?2a2k[(k?1)a2?k]lg|a|

a2?1?2a[k(a?1)?a?2]lg|a|a?1

a2

2k2?2a(a?1)(k?)lg|a|(k?N?).1?a2

2a2722k2当a??时,a?1??,?2a(a?1)lg|a|?0.又?,391?a22

7当k?时,b2k?2?b2k,即b8?b10?b12??;2

7当k?时,b2k?2?b2k,即b8?b6?b4?b2.2

故存在正整数m?8使得对于任意正整数n,都有bn?bm.????12分2k22

8.设数列{an}满足an?0,a1?1，an?(1?2n)anan?1?an?1（n?2），数列{an}的前n项和为Sn.

(1) 求数列{an}的通项公式；

(2) 求证：当n?2时，n?Sn?2； n?1

（3）试探究：当n?2时，是否有6n5?Sn?？说明理由. (n?1)(2n?1)3

（1）解法1：∵an?0

∴anan?1?0（n?2） ∴an(1?2n)anan?1a??n?1-------------------------------------1分 anan?1anan?1anan?1

11?(1?2n)? an?1an

11??2n?1----------------------------------------------------3分 anan?1

∴11111111??(?)?(?)???(?) ana1a2a1a3a2anan?1

n(1?2n?1)?n2（n?2） 2

3 ?1?3?5?7???(2n?1)?

又1?1也适合上式， a1

1 -------------------------------------------------5分 2n∴an?

[解法2：由a1?1，an?(1?2n)anan?1?an?1 得a2?111，a3?，由此猜想an?2，----------------------------------2分 49n

以下用数学归纳法证明：

①当n?1时，由a1?1知猜想显然成立；

②假设当n?k（k?1,k?N?）时猜想成立，即ak?1-----------------------3分 k2

由an?(1?2n)anan?1?an?1得当n?k?1时ak?1?[1?2(k?1)]ak?1ak?ak ak?1?1(?1?2k)1a?a? ∴ k?1k?1k2k2(k?1)2

这就是说当n?k?1时猜想也成立

综①②证明得an?

分]

（2）证明：∵an?1-------------------------------------------------------52n1 n2

∴Sn?a1?a2???an?1?

∵当n?2时，111???? 2232n21111??? n2(n?1)nn?1n

＝∴1?11111111?????1?[(1?)?(?)???(?)]2232n2223n?1n?1

2?1?2------8分 n?1

又∵1111??? n2n(n?1)nn?1

1

211111n)?1?? 23nn?1n?1n?1

n?Sn?2.---------------------------------------------10∴当n?2时，n?1∴Sn?(1?)?(?)???(?

分

4

(3)∵14411???2(?) 22n4n(2n?1)(2n?1)2n?12n?1∴1?111111111?????1?2[(?)?(?)???(?)] 22223n35572n?12n?1

525?-----------------------------------------------------12＝?32n?13

分

当n?2时,要Sn?6nn6n只需 ?(n?1)(2n?1)n?1(n?1)(2n?1)即需2n?1?6，显然这在n?3时成立 而S2?1?6n6?241554?,当n?2时?? 显然? 4544(n?1)(2n?1)(2?1)(4?1)5

6n也成立 (n?1)(2n?1)

6n5?Sn?.------------------------------14(n?1)(2n?1)3即当n?2时Sn?综上所述：当n?2时，有

分

9.已知数列{an}的前n项和Sn?

（1）求{an}的通项公式； 3(an?1)，n?N?． 2

（2）设n?N+，集合An?{y|y?ai,i?n,i?N?}，B?{y|y?4m?1,m?N?}．现在集合An中随机取一个元素y，记y?B的概率为p(n)，求p(n)的表达式． 解：（1）因为Sn?33(an?1)，n?N?，所以Sn?1?(an?1?1)． 22

33两式相减，得Sn?1?Sn?(an?1?an)，即an?1?(an?1?an)， 22

∴an?1?3an，n?N?．??????????3分 又S1?33(a1?1)，即a1?(a1?1)，所以a1?3． 22

∴{an}是首项为3，公比为3的等比数列．

从而{an}的通项公式是an?3n，n?N?．?????????6分

（2）设y?ai?3i?An，i?n，n?N?．

当i?2k，k?N?时，

0k1k?1k?1k∵y?32k?9k?(8?1)k?Ck 8?Ck8???Ck8?Ck

0k?11k?2k?1 ?4?2(Ck8?Ck8???Ck)?1，∴y?B． ?????????9分

5

当i?2k?1，k?N?时，

k?2k?10k?11k?2∵y?32k?1?3?(8?1)k?1?3?(Ck?Ck???Ck?18?18?18?Ck?1)

0k?21k?3?2 ?4?6(Ck?Ck???Ckk??18?181)?3，∴y?B．???????12分

又∵集合An含n个元素，

?1n为偶数,?2 ,

∴在集合An中随机取一个元素y，有y?B的概率p(n)??．???? n?1? , n为奇数.?2n

11.某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策，制定了如下实施方案：20xx年底通过农民个人投保和政府财政投入，共集资1000万元作为全县农村医保基金，从20xx年起，每年报销农民的医保费都为上一年底医保基金余额的10%，并且每年底县财政再向医保基金注资m万元(m为正常数).

（Ⅰ）以20xx年为第一年，求第n年底该县农村医保基金有多少万元？

（Ⅱ）根据该县农村人口数量和财政状况，县政府决定每年年底的医保基金要逐年增加，同

时不超过1500万元，求每年新增医保基金m(单位：万元)应控制在什么范围内.

【解】（Ⅰ）设第n年底该县农村医保基金为an万元，则

a1?1000，an?(1?10%)an?1?m(n?2)，即an?

分） 于是an?10m?9an?1?m(n?2). （31099(an?1?10m)(n?2). 所以an?10m?(a1?10m)()n?1， 1010

9n?1即an?10m?(1000?10m)(). （610

分）

故第n年底该县农村医保基金有10m?(1000?10m)(9n?1)万元. （710

分）

（Ⅱ）若每年年底的医保基金逐年增加，则数列{an}单调递增. 因为y?(

分） 又an?10m?(1000?10m)(9n?1)是减函数，则1000－10m＜0时，即m＞100. （10109n?1)?1500恒成立，则liman?1500. n??10

即10m≤1500，所以m≤150. （12分）

故每年新增医保基金m的控制范围是(100，150]. （13分）

12.已知数列{an}满足a1?2,an?1?an?1. n(n?1)

（I）求数列

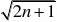
（Ⅱ）设bn?

{an}的通项公式； 1,Tn?b1?b2?b3?bn,求证Tn?1. a2n6

解：（I）由已知得an?1?an??1,又a1?2 n(n?1)

?n?2时,

an?a1?(a2?a1)?(a3?a2)???(an?an?1)

?2?11111111?????2?(1???????)1?22?3(n?1)?n223n?1n

11n?1?2?(1?)?1??nnn a1?2也适合上式

*所以，对一切n?N,an?n?1 ??????6分 n

（II）因bn?

2bn?(2n，所以 2n?12n22n2n2n?12n)????2n?12n?12n?12n2n?1

2462n222?Tn2?b12?b2?b32?bn?()2?()2?()2?() 3572n?1

1234562n?12n1???????

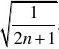
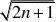
??2345672n2n?12n?1

?Tn?Tn?1 ??????13分

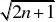
（也可以用数学归纳法或令An?Tn利用数列单调性证明）

3{a}f(x)?ax?3[(t?1)an?an?1]x?1(n?2)的一个极x?nn?113.已知数列，

且是函数

2{a}a?t,a?tn12值点．数列中（t?0且t?1）．

（1）求数列{an}的通项公式；

1an，当t?2时，数列{bn}的前n项和为Sn，求使Sn?2010的n的bn?2(1?

（2）记

最小值；

3nlogtanc2c3cn4??? (n?N*)cn?nn33?1，证明：23（3）若。

'2f(x)?3ax?3[(t?1)an?an?1]，

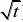
n?1解：（1）

'f?3an?1t?3[(t?1)an?an?1]?0。整理得：an?1?an?t(an?an?1)。 所以

7

{a?an?1}是常数列，得an?1； 当t?1时，n

2{a?a}a?a?t?t为首项，t为公比的等比数列，所以 t?1nn?121当时，是以

an?an?1?(t2?t)?tn?2?(t?1)?tn?1

方法一：由上式得(an?an?1)?(an?1?an?2)???(a2?a1)?(t?1)(tn?1?tn?2???t)，即

t?tn

an?a1?(t?1)??tn?tna?t (n?2)。 1?t，所以n

n*a?t (n?N)。?????4分 t?1又，当时上式仍然成立，故n

nn?1nna?t?a?t{a?t}a?t?a1?t?0，nn?1nn方法二：由上式得：，所以是常数列，

an?tn (n?2)。又，当t?1时上式仍然成立，故an?tn (n?N*)。

2(2n?1)1bn??2?2n2n?1 （2）当t=2时，

1

n111?Sn?2n?(1??2???n?1)?2n?12221?2

11?2n?2(1?n)?2n?2?2?n.22 1?

112n?2?2()n?2010n?()n?1006S?2010，得22由n，， 11n?1005时,n?()n?1006,当n?1006时,n?()n?100622当，

因此n的最小值为1006．

?????8分n?3n3cn?nc1?2，所以 3?1且（3）

cc2c3cn4ccc1111????1?2?3?n?2?(1?)(1?2)?(1?n)?23n3123n3332

8

1?

因为1?3n(1?111111111)(1?)1???1???1?nn?1?n?1n2n?1?nn2n?1?n1?n?11?n?11?n?11?n?13333，

11111?1?21?n1?n111?????1(1?)(1?2?)?n??3331?11?221?n?133所以，从而原命题得

证???14分

14已知数列{an}是等比数列，Sn为其前n项和．（1）若S4，S10，S7成等差数列，证明a1，a7，a4也成等差数列；

321（2）设S3?，S6?，bn??an?n2，若数列{bn}是单调递减数列，求实数?的取216

值范围．

（1）设数列{an}的公比为q，

因为S4，S10，S7成等差数列，所以q?1，且2S10?S4?S7．

2a11?q10a11?q4a11?q7

所以， ??1?q1?q1?q

因为q?0，所以1?q3?2q6． ????????????????4分 所以a1?a1q3?2a1q6，即a1?a4?2a7．

所以a1,a7,a4也成等差数列． ??????????????????6分

（2）因为S3???????321，S6?， 216

a11?q33所以?，????????① 1?q2

a11?q621?，????????② 1?q16

3由②?①，得1?q?????71，所以q??，代入①，得a1?2． 82

， ?????????????????????8分 ?1?所以an?2?????2?n?1

9

?1?又因为bn??an?n2，所以bn?2?????2?n?1?n2，

由题意可知对任意n?N*，数列{bn}单调递减，

所以bn?1?1??1??bn，即2??????n?1?2?2?????2??2?

nnn?1?n2， ?1?即6?????2n?1对任意n?N*恒成立， ????????????10分 ?2?

(2n?1)2n(2n?1)2n

当n是奇数时，???，当n?1时，?取得最大值－１， 66

所以???1； ????????????????????????12分

(2n?1)2n(2n?1)2n10当n是偶数时，?? ，当n?2时，取得最小值， 366

所以??10． 3

1010，即实数?的取值范围是(?1,)．????14分 33综上可知，?1???

17.设等差数列{an}的前n项和为Sn，且a5?a13?34，S3?9．

（1）求数列{an}的通项公式及前n项和公式；

（2）设数列{bn}的通项公式为bn?an，问: 是否存在正整数t，使得b1，b2，bm an?t

(m?3，m?N)成等差数列？若存在，求出t和m的值；若不存在，请说明理由.

【解】（1）设等差数列{an}的公差为d. 由已知得??a5?a13?34， ????????2分 3a?9，?2

即??a1?8d?17，?a1?1，，Sn?n2. ???6分 解得?????????4分.故an?2n?1?d?2.?a1?d?3，

（2）由（1）知bn?2n?1.要使b1，b2，bm成等差数列，必须2b2?b1?bm，即2n?1?t

2?4312m?1，??8分.整理得m?3?， ????? 11分 ?t?13?t1?t2m?1?t

因为m，t为正整数，所以t只能取2，3，5.当t?2时，m?7；当t?3时，m?5；当t?5时，m?4.

故存在正整数t，使得b1，b2，bm成等差数列. ??????? 15分

10

19. 设函数f?x???1?2x?3*x?0，数列满足 an?a1?1,an?f?n?N,且n?2．????3x?an?1???

⑴求数列?an?的通项公式；

⑵设Tn?a1a2?a2a3?a3a4?a4a5???????1?

求实数t的取值范围；

*⑶是否存在以a1为首项，公比为q0?q?5,q?N的数列ank，k?N*，使得数n?1anan?1，若Tn?tn2对n?N*恒成立，????

列ank中每一项都是数列?an?中不同的项，若存在，求出所有满足条件的数列?nk?的通项公式；若不存在，说明理由． ??

1?3?1?an?12??a?,?n?N*,且n?2?， 解：⑴因为an?f??n?13?an?1?3?an?12?

2．????????????????????????????2分 3

2因为a1?1，所以数列?an?是以1为首项，公差为的等差数列． 3

2n?1所以an?．????????????????????????????4分 3所以an?an?1?

⑵①当n?2m,m?N*时，

Tn?T2m?a1a2?a2a3?a3a4?a4a5???????1?2m?1a2ma2m?1

?a2?a1?a3??a4?a3?a5??????a2m?a2m?1?a2m?1?

??44a?a1?a2?a4???a2m????22m?m???8m2?12m? 3329

1???2n2?6n?．????????????????????????????6分 9

②当n?2m?1,m?N*时，

Tn?T2m?1?T2m???1?2m?1a2ma2m?1

??118m2?12m???16m2?16m?3? ?99

11??8m2?4m?3???2n2?6n?7?．????????????????8分 99

11

?12?2n?6n?,n为偶数，???9所以Tn??

?1?2n2?6n?7?，n为奇数??9

要使Tn?tn2对n?N*恒成立， 只要使?12n2?6n??tn2,(n为偶数)恒成立． ?9

只要使??2?1?

9?6???t,对n为偶数恒成立， n?

?

?5??故实数t的取值范围为???，??．????????????????????10分 9

⑶由an?2n?1，知数列?an?中每一项都不可能是偶数． 3

①如存在以a1为首项，公比q为2或4的数列ank，k?N*，

此时ank中每一项除第一项外都是偶数，故不存在以a1为首项，公比为偶数的数列????

?a?．????????????????????????????????12分 nk

②当q?1时，显然不存在这样的数列ank．

*当q?3时，若存在以a1为首项，公比为3的数列ank，k?N． ????

则an1?1，n1?1，ank?3k?12nk?13k?1?，nk?． 32

3k?1所以满足条件的数列?nk?的通项公式为nk?．??????????????16分 2

20. 已知数列{an}、{bn}中,对任何正整数n都有：

a1bn?a2bn?1?a3bn?2???an?1b2?anb1?2n?1?n?2．

(1)若数列{an}是首项和公差都是1的等差数列,求证：数列{bn}是等比数列；

(2)若数列{bn}是等比数列,数列{an}是否是等差数列,若是请求出通项公式,若不是请说明理由；

12

(3)若数列{an}是等差数列,数列{bn}是等比数列,求证：解：（1）依题意数列{an}的通项公式是an?n， 13． ??2i?1aibin

故等式即为bn?2bn?1?3bn?2???(n?1)b2?nb1?2n?1?n?2， bn?1?2bn?2?3bn?3???(n?2)b2?(n?1)b1?2n?n?1?n?2?， 两式相减可得bn?bn?1???b2?b1?2n?1 ----------- -------3分 得bn?2n?1，数列{bn}是首项为1，公比为2的等比数列． -------4分

（2）设等比数列{bn}的首项为b，公比为q，则bn?bqn?1，从而有：

bqn?1a1?bqn?2a2?bqn?3a3???bqan?1?ban?2n?1?n?2， 又bqn?2a1?bqn?3a2?bqn?4a3???ban?1?2n?n?1?n?2?， 故(2n?n?1)q?ban?2n?1?n?2 ------------------------6分 an?2?qnq?1q?2?2??n?， bbb

要使an?1?an是与n无关的常数，必需q?2， ---------------------8分 即①当等比数列{bn}的公比q?2时，数列{an}是等差数列，其通项公式是an?②当等比数列{bn}的公比不是2时，数列{an}不是等差数列． ---9分

（3）由（2）知anbn?n?2n， ---------------------------- --------------10分

显然n?1,2时n； b13? ?ab2i?1iin

当n?3时111111??????? ?23n?11?12?23?24?2n?2i?1aibi

＜n11111?????? -----14分 1?12?22?222?232?2n?1

11?()n?1

1313??n? -----------------16分 ?1??12222?21?2

21.已知各项均为整数的数列?an?满足：a9??1，a13?4，且前12项依次成等差数列，从 13

第11项起依次成等比数列．

（1）求数列?an?的通项公式；

（2）若存在正整数m、p使得：am?am?1???am?p?amam?1?am?p，请找出所有的有序数对(m,p)，并证明你的结论．

解：（1）设由前12项构成的等差数列的公差为d，从第11项起构成的等比数列的公比为q， ?q?62?q?2?a12(?1?3d)2

由a13?或???4可得?5， d?1a11?1?2dd???9?

又数列?an?各项均为整数，故? （3分） ?q?2?n?10,n?12；所以an??n?11n?N?； （6分）

?d?1?2,n?13

（2）数列?an?为：?9,?8,?7,?6,?5,?4,?3,?2,?1,0,1,2,4,8,16,?

当am,am?1,???,am?p均为负数时，

显然am?am?1?????am?p?0，所以amam?1???am?p?0，即am,am?1,???,am?p共有奇数项，即p为偶数；又最多有9个负数项，所以p?8，

p?2时，经验算只有(?3)?(?2)?(?1)?(?3)?(?2)?(?1)符合，此时m?7； p?4,6,8时，经验算没有一个符合；

故当am,am?1,?,am?p均为负数时，存在有序数对(7,2)符合要求．

当am,am?1,???,am?p均为正数时，m?11且m?N， ? （8分）

am?am?1?????am?p?2m?11?2m?10?????2m?p?11

?2m?11(1?2?????2p)?2m?11(2p?1?1)

amam?1???am?p?2

因为2p?1m?11?2m?10?????2m?p?11?(2m?11p)?21?2?????p?(2m?11p)?2(p?1)p2 ?1是比1大的奇数，所以am?am?1?????am?p能被某个大于1的奇数（2p?1?1）

m?11p整除，而(2)?2(p?1)p

2不存在大于1的奇约数，故am?am?1?????am?p?amam?1?am?p；

（11分） 故当am,am?1,???,am?p均为正数时，不存在符合要求有序数对；

14

当am,am?1,???,am?p中既有正数又有负数，即am,am?1,???,am?p中含有0时， 有amam?1???am?p?0，所以am?am?1?????am?p?0，

（方法一）设负数项有k(k?N?,且k?9)，正数项有l(l?N?)， 则am,am?1,???,am?p应是?k,?(k?1),?(k?2),???,?2,?1,0,1,2,?,2l?1， 故有k(k?1)?2l?1；经验算： 2

k?1时，l?1，此时am,am?1,???,am?p为?1,0,1，m?9,p?2； k?2时，l?2，此时am,am?1,???,am?p为?2,?1,0,1,2，m?8,p?4； k?5时，l?4，此时am,am?1,???,am?p为?5,?4,?3?2,?1,0,1,2,4,8，m?5,p?9； k?3,4,6,7,8,9时，均不存在符合要求的正整数l；

故当am,am?1,???,am?p中既有正数又有负数时，存在三组有序数对(9,2)，(8,4)，(5,9)符合要求；

（方法二）因为负数项只有九项，我们按负数项分类：

含1个负数项时，?1,0,1，符合，此时m?9,p?2；

含2个负数项时，?2,?1,0,1,2，符合，此时m?8,p?4；

含3个或4个负数项时，经验算不存在符合要求的；

含5个负数项时， ?5,?4,?3?2,?1,0,1,2,4,8，符合，此时m?5,p?9； 含6个及6个以上负数项时，经验算不存在符合要求的；

故当am,am?1,???,am?p中既有正数又有负数时，存在三组有序数对(9,2)，(8,4)，(5,9)符合要求；

综上，存在四组有序数对(9,2)，(8,4)，(5,9)，(7,2)符合要求． （注：只找出有序数对无说明过程，一个有序数对只给1分）

22.已知数列{an}是以d为公差的等差数列，数列{bn}是以q为公比的等比数列． （Ⅰ）若数列{bn}的前n项和为Sn,且a1?b1?d?2,S3?a1003?5b2?2010,求整数q的值；

（Ⅱ）在（Ⅰ）的条件下，试问数列{bn}中是否存在一项bk，使得bk恰好可以表示为

该数列中连续p(p?N,p?2)项的和？请说明理由；

（Ⅲ）若b1?ar,b2?as?ar,b， 3?at（其中t?s?r，且（s?r）是（t?r）的约数）

求证：数列{bn}中每一项都是数列{an}中的项.

15 （16分）

解：（Ⅰ）由题意知，an?2n,bn?2?qn?1，所以由S3?a1003?5b2?2010， 得

b1?b2?b3?a1003?5b2?2010?b1?4b2?b3?2006?2010?q2?4q?3?0……3分

解得1?q?3，又q为整数，所以

q?2………………………………………………………5分

（Ⅱ）假设数列?bn?中存在一项bk，满足bk?bm?bm?1?bm?2?????bm?p?1， 因为bn?2n

k，∴bk?bm?p?1?2k?2m?p?1?k?m?p?1?k?m?pmm?1n?p?1（*）…………8分 2m(2p?1)? 又bk?2?bm?bm?1?bm?2?????bm?p?1?2?2?????2 2?1

m?p?2m?2m?p，=2所以k?m?p，此与（*）式矛盾. 所以，这要的项bk不存在……11分

（Ⅲ）由b1?ar，得b2?b1q?arq?as?ar?(s?r)d，则

d?ar(q?1) ………………12分 s?r

222 又b3?b1q?arq?at?ar?(t?r)d?arq?ar?(t?r)?ar(q?1)， s?r

从而ar(q?1)(q?1)?ar(q?1)?t?r，因为as?ar?b1?b2，所以q?1，又s?r

ar?0， t?r?1. 又t?s?r,且（s?r）是（t?r）的约数,所以q是整数,且故q?s?r

q?2………14分

对于数列{bn}中任一项bi（这里只要讨论i?3的情形），有

bi?arqi?1?ar?ar(qi?1?1)

?ar?ar(q?1)(1?q?q2?????qi?2)?ar?d(s?r)(1?q?q2?????qi?2) ?ar?[((s?r)(1?q?q2?????qi?2)?1)?1]?d，

由于(s?r)(1?q?q?????q

分

23.已知数列{an}，an?pn??qn(p?0,q?0,p?q,??R,??0,n?N*). ⑴求证：数列{an?1?pan}为等比数列；

⑵数列{an}中，是否存在连续的三项，这三项构成等比数列？试说明理由； ⑶设A?{(n,bn)|bn?3n?kn,n?N*}，其中k为常数，且k?N， ?2i?2)?1是正整数，所以bi一定是数列{an}的项……………16

16

B?{(n,cn)|cn?5n,n?N*}，求A?B.

解：⑴∵an=pn??qn，∴an?1?pan?pn?1??qn?1?p(pn??qn)??qn(q?p)， ∵??0,q?0,p?q∴

分

⑵取数列{an}的连续三项an,an?1,an?2(n?1,n?N?)，

2n?1∵an??qn?1)2?(pn??qn)(pn?2??qn?2)???pnqn(p?q)2， ?1?anan?2?(pan?2?pan?1?q为常数∴数列{an?1?pan}为等比数列------------4an?1?pan

2?p?0,q?0,p?q,??0，∴??pnqn(p?q)2?0，即an?1?anan?2，

∴数列{an}中不存在连续三项构成等比数列； --------------------9分

nnnn⑶当k?1时，3?k?3?1?5，此时B?C??；

nnnnnn当k?3时，3?k?3?3?2?3为偶数；而5为奇数，此时B?C??；

nnn当k?5时，3?k?5，此时B?C??；----------------------------------------------12分

当k?2时，3n?2n?5n，发现n?1符合要求，下面证明唯一性（即只有n?1符合要求）。

32

55

3x2x3x2x设f(x)?()?()，则f(x)?()?()是R上的减函数，∴ f(x)?1的解只有一5555nnnnn由3?2?5得()?()?1， 个

nnnnn从而当且仅当n?1时()?()?1，即3?2?5，此时B?C?{(1,5)}； 3

525

nnn当k?4时，3?4?5，发现n?2符合要求，下面同理可证明唯一性（即只有n?2符

合要求）。

34

55

综上，当k?1，k?3或k?5时，B?C??；

当k?2时，B?C?{(1,5)}， nnnnn从而当且仅当n?2时()?()?1，即3?4?5，此时B?C?{(2,25)}；

当k?4时，B?C?{(2,25)}。 ------------------------------16分

x2

24.已知函数f(x)?的图像经过点(4,8). x?m

（1）求该函数的解析式；

17

（2）数列?an?中，若a1?1，Sn为数列?an?的前n项和，且满足an?f(Sn)(n≥2)， 证明数列??1??成等差数列，并求数列?an?的通项公式；

?Sn?

（3）另有一新数列?bn?，若将数列?bn?中的所有项按每一行比上一行多一项的规则排成

如下数表：

b1

b2 b3

b4 b5 b6

b7 b8 b9 b10

…………

记表中的第一列数b1，b2，b4，b7，...,构成的数列即为数列?an?，上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数．当 b81??

4时，求上表中第k(k≥3)行所有项的和． 91

18

19

20