高考数列专题总结(全是精华)
数列专题复习(0929)
一、证明等差等比数列
1. 等差数列的证明方法:
(1)定义法: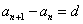 (常数) (2)等差中项法:
(常数) (2)等差中项法: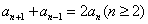
2.等比数列的证明方法:
(1)定义法: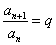 (常数) (2)等比中项法:
(常数) (2)等比中项法:
例1.设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,
Tn为数列{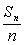 }的前n项和,求Tn.
}的前n项和,求Tn.
解:设等差数列{an}的公差为d,则
Sn=na1+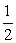 n(n-1)d.∴S7=7,S15=75,∴
n(n-1)d.∴S7=7,S15=75,∴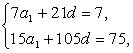 即
即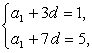
解得a1=-2,d=1.∴ =a1+
=a1+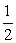 (n-1)d=-2+
(n-1)d=-2+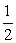 (n-1).
(n-1).
∵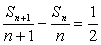 ,∴数列{
,∴数列{ }是等差数列,其首项为-2,公差为
}是等差数列,其首项为-2,公差为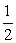 ,
,
∴Tn=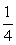 n2-
n2-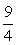 n.
n.
例2.设数列{an}的首项a1=1,前n项和Sn满足关系式:
3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…)
求证:数列{an}是等比数列;
解:(1)由a1=S1=1,S2=1+a2,得a2=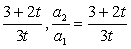
又3tSn-(2t+3)Sn-1=3t ①
3tSn-1-(2t+3)Sn-2=3t ②
①-②得3tan-(2t+3)an-1=0 ∴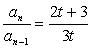 ,(n=2,3,…)
,(n=2,3,…)
所以{an}是一个首项为1,公比为 的等比数列.
的等比数列.
练习:已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
答案 .(2)  ,
, ;
;
二.通项的求法
(1)利用等差等比的通项公式
(2)累加法:
例3.已知数列 满足
满足 ,
, ,求
,求 。
。
解:由条件知:
分别令 ,代入上式得
,代入上式得 个等式累加之,即
个等式累加之,即
 所以
所以
 ,
,
(3)构造等差或等比 或
或
例4.已知数列 满足
满足
求数列 的通项公式;
的通项公式;
解:

 是以
是以 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。

即 
例5.已知数列 中,
中, ,
, ,求
,求 .
.
解:在 两边乘以
两边乘以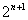 得:
得:
令 ,则
,则 ,解之得:
,解之得: ,所以
,所以 .
.
练习:已知数列 满足
满足 ,且
,且 。
。
(1)求 ; (2)求数列
; (2)求数列 的通项公式。
的通项公式。
解: (1)
(2)

∴
(4)利用
例6.若 和
和 分别表示数列
分别表示数列 和
和 的前
的前 项和,对任意正整数
项和,对任意正整数
 ,
, .求数列
.求数列 的通项公式;
的通项公式;
解: 
 ……2分 当
……2分 当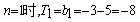
当 ……4分
……4分
练习:1. 已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列,求数列{an}的通项an
解: ∵10Sn=an2+5an+6, ① ∴10a1=a12+5a1+6,解之得a1=2或a1=3
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2)
当a1=3时,a3=13,a15=73 a1, a3,a15不成等比数列∴a1≠3;
a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3
2.设数列 的前
的前 项的和
项的和
 ,
,
(Ⅰ)求首项 与通项
与通项 ;
;
(Ⅱ)设 ,
, ,证明:
,证明:
解:(I) ,解得:
,解得:


所以数列 是公比为4的等比数列
是公比为4的等比数列
所以:
得: (其中n为正整数)
(其中n为正整数)
(II)

所以: 
(5)累积法  转化为
转化为 ,逐商相乘.
,逐商相乘.
例7.已知数列 满足
满足 ,
, ,求
,求 。
。
解:由条件知 ,分别令
,分别令 ,代入上式得
,代入上式得 个等式累乘之,即
个等式累乘之,即



又 ,
,
练习:1.已知 ,
,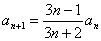
 ,求
,求 。
。
解:
 。
。
2.已知数列{an},满足a1=1, (n≥2),
(n≥2),
则{an}的通项

解:由已知,得 ,用此式减去已知式,得
,用此式减去已知式,得
当 时,
时, ,即
,即 ,又
,又 ,
,
 ,将以上n个式子相乘,得
,将以上n个式子相乘,得

(6)倒数变形: ,两边取倒数后换元转化为
,两边取倒数后换元转化为 。
。
例8:已知数列{an}满足: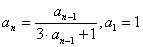 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
解:取倒数:
 是等差数列,
是等差数列,


练习:已知数列{an}满足:a1=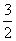 ,且an=
,且an=
求数列{an}的通项公式;
解:将条件变为:1- =
=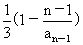 ,因此{1-
,因此{1- }为一个等比数列,其首项为
}为一个等比数列,其首项为
1-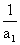 =
= ,公比
,公比 ,从而1-
,从而1- =
= ,据此得an=
,据此得an= (n³1)
(n³1)
三.数列求和
1、等差数列求和公式:
2、等比数列求和公式:
3、错位相减法求和
{ an }、{ bn }分别是等差数列和等比数列.
例9. 求和:
解:由题可知,设 ………………………①
………………………①
 …②(设制错位)
…②(设制错位)
①-②得  (错位相减)再利用等比数列的求和公式得:
(错位相减)再利用等比数列的求和公式得: 。
。
∴ 
练习: 求数列 前n项的和.
前n项的和.
解:由题可知,{ }的通项是等差数列{2n}的通项与等比数列{
}的通项是等差数列{2n}的通项与等比数列{ }的通项之积
}的通项之积
设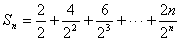 …………………………………①
…………………………………①
 …………② ①-②得
…………② ①-②得

∴ 
4、倒序相加法求和
这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个 .
.
5、分组法求和
有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.
例10. 求数列的前n项和: ,…
,…
解:设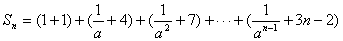
将其每一项拆开再重新组合得
 (分组)
(分组)
当a=1时, =
= (分组求和)
(分组求和)
当 时,
时, =
=
6、裂项法求和
这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)
(1) 为等差数列,
为等差数列,
(2)
例11. 求数列 的前n项和.
的前n项和.
解:设 ,则
,则


=
例12. 在数列{an}中, ,又
,又 ,求数列{bn}的前n项的和.
,求数列{bn}的前n项的和.
解: ∵ 
∴ 
 数列{bn}的前n项和:
数列{bn}的前n项和:
 =
= =
= 
练习:
1.已知数列{ }的前
}的前 项和为
项和为 ,且满足
,且满足 。求数列{
。求数列{ }的通项公式;
}的通项公式;
解:(1)数列{ }的前
}的前 项和为
项和为 ,且满足
,且满足
则 (
( )
)
相减得:

 (
( )
)
又当n=1时, ,
, ,
,
 {
{ }是以
}是以 为首项,公比
为首项,公比 的等比数列
的等比数列
 (
( )
)
2.已知数列 :
:
①求证数列 为等差数列,并求它的公差
为等差数列,并求它的公差
②设 ,求
,求 。
。
解:①由条件,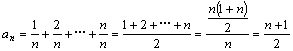
∴ ;∴
;∴
故 为等差数列,公差
为等差数列,公差
②
又知
∴

第二篇:高考数列专题总结(全是精华)
数列复习
一、证明等差等比数列
1. 等差数列的证明方法:
(1)定义法: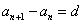 (常数) (2)等差中项法:
(常数) (2)等差中项法: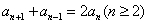
2.等比数列的证明方法:
(1)定义法: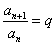 (常数) (2)等比中项法:
(常数) (2)等比中项法: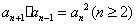
例1.设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,
Tn为数列{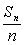 }的前n项和,求Tn.
}的前n项和,求Tn.
例2.设数列{an}的首项a1=1,前n项和Sn满足关系式:
3tSn-(2t+3)Sn-1=3t(t>0,n=2,3,4,…)
求证:数列{an}是等比数列;
练习:已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1) 证明数列{lg(1+an)}是等比数列;
(2) 设Tn=(1+a1) (1+a2) …(1+an),求Tn及数列{an}的通项;
二.通项的求法
(1)利用等差等比的通项公式
(2)累加法: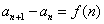
例3.已知数列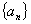 满足
满足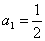 ,
,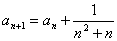 ,求
,求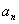 。
。
例4.已知数列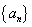 满足
满足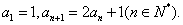
求数列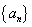 的通项公式;
的通项公式;
例5.已知数列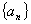 中,
中,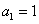 ,
,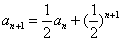 ,求
,求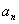 .
.
练习:已知数列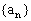 满足
满足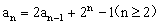 ,且
,且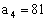 。
。
(1)求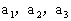 ; (2)求数列
; (2)求数列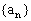 的通项公式。
的通项公式。
例6.若 和
和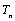 分别表示数列
分别表示数列 和
和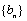 的前
的前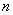 项和,对任意正整数
项和,对任意正整数
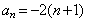 ,
, .求数列
.求数列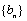 的通项公式;
的通项公式;
练习:1. 已知正项数列{an},其前n项和Sn满足10Sn=an2+5an+6且a1,a3,a15成等比数列,求数列{an}的通项an
2.设数列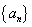 的前
的前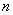 项的和
项的和
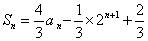 ,
,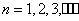
(Ⅰ)求首项 与通项
与通项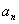 ;
;
(Ⅱ)设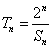 ,
,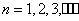 ,证明:
,证明:
例7.已知数列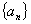 满足
满足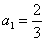 ,
,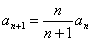 ,求
,求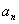 。
。
练习:1.已知 ,
,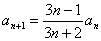
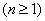 ,求
,求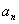 。
。
2.已知数列{an},满足a1=1, (n≥2),
(n≥2),
则{an}的通项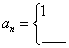
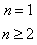
倒数变形: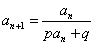 ,两边取倒数后换元转化为
,两边取倒数后换元转化为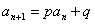 。
。
例8:已知数列{an}满足: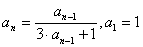 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
练习:已知数列{an}满足:a1= ,且an=
,且an=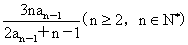
求数列{an}的通项公式;
三.数列求和
1、等差数列求和公式: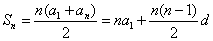
2、等比数列求和公式:
3、错位相减法求和
{ an }、{ bn }分别是等差数列和等比数列.
例9. 求和:
练习: 求数列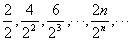 前n项的和.
前n项的和.
4、倒序相加法求和
这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个 .
.
5、分组法求和
有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.
例10. 求数列的前n项和: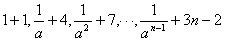 ,…
,…
6、裂项法求和
这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)
(1)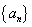 为等差数列,
为等差数列,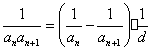
(2)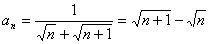
例11. 求数列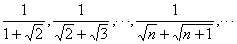 的前n项和.
的前n项和.
例12. 在数列{an}中,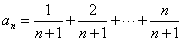 ,又
,又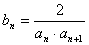 ,求数列{bn}的前n项的和.
,求数列{bn}的前n项的和.
练习:
1.已知数列{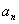 }的前
}的前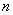 项和为
项和为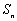 ,且满足
,且满足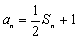 。求数列{
。求数列{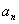 }的通项公式;
}的通项公式;
2.已知数列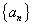 :
: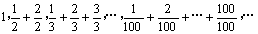
①求证数列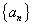 为等差数列,并求它的公差
为等差数列,并求它的公差
②设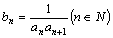 ,求
,求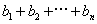 。
。
-
高考数列专题总结(全是精华)
数列专题复习(0929)一、证明等差等比数列1.等差数列的证明方法:(1)定义法:an?1?an?d(常数)(2)等差中项法:an…
-
高考数列专题总结(全精华)
数列专题复习一证明等差等比数列1等差数列的证明方法1定义法an1and常数2等差中项法an1an12ann22等比数列的证明方法1…
-
高考文科数列知识点总结(全)
数列知识点二知识点一数列的该概念和表示法1数列定义按一定次序排列的一列数叫做数列数列中的每个数都叫这个数列的项记作an在数列第一个…
-
高考数列专题总结(全精华)
数列专题复习全是精华一证明等差等比数列1等差数列的证明方法1定义法an1and常数2等差中项法an1an12ann22等比数列的证…
-
高考文科数列知识点总结
一等差数列1等差数列的定义anan1dd为常数n22等差数列通项公式ana1n1ddna1dnN首项a1公差d末项an推广anam…
-
高中数学数列知识点总结
数列一、数列定义:数列是按照一定次序排列的一列数,是定义在正整数集N(或它的有限子集*{1,2,3,?,n})上的函数f(n),当…
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y…
-
-数列常见题型总结 -
--数列(常见、常考题型总结)题型一:求值类的计算题(多关于等差等比数列)A)根据基本量求解(方程的思想)1、已知Sn为等差数列?…
-
20xx年高考数学数列知识点大总结
20xx年高考数学数列知识点及题型大总结等差数列知识要点1.递推关系与通项公式递推关系:an?1?an?d通项公式:an?a1?(…
-
等比数列知识点总结及题型归纳
1、等比数列的定义:2、通项公式:an?a1qn?1?a1nq?A?Bn?a1?q?0,A?B?0?,首项:a1;公比:qqan?…
-
数列总结
第二章数列1.数列与函数从概念上理解为:数列是一种不连续的函数集,如下图所示两者的区别:函数是连续的,而数列是离散的,而且其自变量…