“数学归纳法”教学设计

一、教材与内容解析

（一）内容与内容解析

数学归纳法是人教B版普通高级中学教科书数学选修2-2第二章第三节的内容。本节课的主要内容是介绍数学归纳法的原理。

由于正整数具有无穷无尽的特点，有些关于正整数n的命题,难以对n进行一一的验证，从而需要寻求一种新的推理方法，以便能通过有限的推理来证明无限的结论，这是数学归纳法产生的根源。
　　数学归纳法是一种证明与正整数n有关命题的重要方法。它的独到之处便是运用有限个步骤就能证明无限多个对象，而实现这一目的的工具就是递推思想。
    数学归纳法的两个步骤中，第一步是证明的奠基，第二步是递推。递推是实现从有限到无限飞跃的关键，没有它我们就只能停留在对有限情况的把握上。

数学归纳法是以归纳为基础、以演绎为手段证明结论的一种方法，是归纳法与演绎法的完善结合．这也许是数学归纳法不是归纳法但又叫“数学归纳法”的原因．

（二）地位与作用解析

从应用上看，数学归纳法是解决与正整数有关命题的一种推理方法，它将无限多个归纳过程转化为一个有限步骤的演绎过程，是证明与正整数有关问题的重要工具。数学归纳法本质是归纳递推，但它与归纳法有着一定程度的关联。在数学结论的发现过程中，不完全归纳法发现结论，最终利用数学归纳法证明解决问题。

从思想方法上看，数学归纳法蕴含了无限转化为有限的思想，体现了奠基、递推、总结一体的整体思想。

从美学上看，数学归纳法展现了无限与有限的统一美；揭示了有限推证无限，把无限“沦为”有限的思维美；数学归纳法的发展历程展现了数学文化美。

二、教学问题诊断

1．学生已有的经验和基础：(1)学生已有数学归纳法的萌芽和相关经验．虽然学生没有正式学过数学归纳法，但小学的数数、找一列数的规律、高中等差数列和等比数列通项公式的推导过程等等，都蕴含着数学归纳法的萌芽和基础．(2)学生已经有用具有代表性的元素来代替任意的、无穷多的元素的经验．如在线面垂直的定义和证明中，用“平面内任意一条直线”来代表“平面内所有直线”；在讨论函数奇偶性时，用定义域内任意数来代表定义域内的所有数。(3)学生具有学习数学归纳法的心理需求，如学生希望证明通过归纳推理得到的与正整数有关的命题。（4）学生基本上都知道多米若骨牌效应，但并不清楚其原理以及与数学归纳法的联系。

2．学生可能遇到的问题与困难．(1)对数学归纳法产生源头及其所要证明的问题的特征理解不到位。(2)形成和得到数学归纳法原理时，如何把无穷的不断重复的递推过程用有限的、一般性的步骤来代替学生会有困难。(3)对数学归纳法第二个步骤的作用，尤其是为什么可以根据归纳假设进行证明、如何利用归纳假设进行证明，学生往往难以理解。(4)由于数学思想的形成需要经历萌芽期、明朗期、成熟期，因此学生难以在一节课或几节课内深刻理解数学归纳法的精神实质。(5)学生初学数学归纳法时容易把注意力集中到第二步归纳推理上，而对数学归纳法的整体认识不够。

三、教学重难点解析

  1．重 点

 （1）数学归纳法的原理。

 （2）数学归纳法证明命题的两个步骤

 （3）初步会用数学归纳法证明简单的与正整数有关的数学命题

   2．难 点

  （1）对数学归纳法原理的理解，

四、教学目标解析

 1．知识与技能

   （1）知道由有限多个特殊事例即不完全归纳法得出的结论不一定正确

   （2）能从整体上认识数学归纳法的原理，知道无限转化为有限的递推本质。

   （3）知道数学归纳法的三个步骤之间的关系，能初步学会用数学归纳法证明简单命题。

   2．过程与方法

经历与感受数学归纳法原理发现和提出的过程，体会其中蕴含的化无限问题为有限问题的思路与方法。培养学生观察、归纳、猜想、分析能力和抽象概括能力

   3．情感态度与价值观

     （1）培养学生严谨的、实事求是的科学态度和不怕困难，勇于探索的精神。

     （2）感受数学的统一美、思维美，感受数学发展的历程，树立数学文化观。

     （3）感悟数学与生活的联系

五、教法学法解析

教法解析

（1）引导发现法：通过问题情境发现不完全归纳法所得结论不一定准确；通过生活情境、实验演示情境发现解决与正整数有关命题的方法。

（2）讲解法：教师讲解归纳法的内涵；讲解数学归纳法证明步骤；讲解数学归纳法的主要发展历程。

学法解析

以问题为中心，以解决问题为主线展开，学生参与观察、分析、归纳、概括、阅读、探究等学习活动。

六、教具准备

 多媒体，黑板

七、教学过程设计

（一）创设情境，引入课题

 情景一：历史的实际例子费马猜测  

设计意图：感悟历史，体会不完全归纳法得到的结论不一定正确，为引出课题奠定基础。

      情景二：证明：当时，成立

设计意图：激发学生探究欲望，引出课题。

（二) 实验演示，探究方法

      1．视频播放——多米诺骨牌游戏

设计意图：感悟生活之美，设计之美，激发学习兴趣

  2．动画演示——多米诺骨牌效应

     师生共同探讨多米诺骨牌全部依次倒下的条件：

    （1）第一块要倒下;    （2）第k块倒下，则第k+1块也倒下

设计意图：转入理性思维，探究无限过程持续原理，为问题解决奠定基础。

      3．思维对接——分析数学问题解决

与命题结合分析：证明：当时，成立

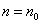        （1）当 时，成立    对接： 时命题成立

        （2）由成立成立  对接：时成立，则时命题成立。

满足这两个条件后，命题对一切n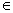均成立。由此归纳出数学归纳法严格的证明步骤。

设计意图：感悟生活现象与数学问题关联性，揭示数学归纳法两个步骤来源，体会无限化有限的本质。实现化解难点。

（三）总结提炼，理解升华

          学生总结用数学归纳法证明命题的三个步骤：

         （1）n取初始值 (例如)时命题成立;

         （2）假设命题成立，证明时命题也成立

         （3）当（1）（2）同时成立时，则能证明出命题成立

设计意图：得出结论，进一步整体理解三个步骤关系，进一步突出重点

（四）运用结论，解决问题

     师生共同用数学归纳法证明：当时，成立

设计意图：初步应用，规范书写，进行解题示范，进一步突出重点

（五）阅读材料，感悟文化

学生阅读数学材料：

古希腊欧几里得证明“素数个数无穷” 已隐含数学归纳法这一推理模式。

证明：设素数个数只有有限多个，由小到大依次为：2，3，5，7，┄，p。

制造一个新数Q=2﹒3﹒5﹒7 ┄ p + 1,显然Q 大于2，3，5，7┄，p中的任何一个。

（i）若Q是素数，则Q不同于2，3，5，7，┄,p中的任何一个，这说明在2，3，5，7，┄,p之外还有一个素数Q，与假设矛盾。

(ii)若Q不是素数，则它一定含有一个素因数设为q，q整除Q，而Q除以2，3，5，7，┄,p中的任何一个，均有余数1，可知q不同于2，3，5，7，┄,p中的任何一个，即在2，3，5，7，┄,p外还有一个素数q，也与假设矛盾。

此证法的关键是制造一个新数Q，从而推知：若有个k素数，就必有k+1个素数。当年欧氏只是用反证法进行证明，到此就止步了。如果他向前迈一步，对解答过程进一步反思：由于有第1个素数，就可以推出有第2个素数；由于有第2个素数，就可以推出有第3个素数；┄┄，如此递推下去，就可以成为数学归纳法的模式。非常可惜，事后经过一千多年，才由意大利科学家莫洛里克斯发现。

Ernest认为：数学归纳法的基本特征在于它用惟一的公式简缩了无穷多个三段论式。数学归纳法发现不仅仅在于人们拥有了一种证明与自然数有关命题的方法，更在于人类拥有了政府无限的能力。数学归纳法之美在于由有限推证无限，把无限“沦为”有限，是一种思维之美，创造之美。

（六）归纳小结，回顾整理

    ? 一种方法：证明某些与正整数有关命题的方法——数学归纳法

    ? 两个注意，一个结论：

      归纳奠基不可少   归纳假设要做到    归纳小结莫忘掉

设计意图：总结学习结果，使知识得以深化。

（七）布置作业，巩固提升

1．用数学归纳法证明： 

2．已知数列  计算，根据计算结果猜想，用数学归纳法证明猜想。

八、板书设计

 

第二篇：数学归纳法的应用习题

第2课时　数学归纳法的应用

1．利用数学归纳法证明＋＋＋…＋<1(n∈N^*，且n≥2)时，第二步由k到k＋1时不等式左端的变化是

(　　)．

A．增加了这一项

B．增加了和两项

C．增加了和两项，同时减少了这一项

D．以上都不对

解析　不等式左端共有n＋1项，且分母是首项为n，公差为1，末项为2n的等差数列，当n＝k时，左端为＋＋＋…＋；当n＝k＋1时，左端为＋＋＋…＋＋＋，对比两式，可得结论．

答案　C

2．用数学归纳法证明“当n为正奇数时，xⁿ＋yⁿ能被x＋y整除”的第二步是

(　　)．

A．假使n＝2k＋1时正确，再推n＝2k＋3正确

B．假使n＝2k－1时正确，再推n＝2k＋1正确

C．假使n＝k时正确，再推n＝k＋1正确

D．假使n≤k(k≥1)，再推n＝k＋2时正确(以上k∈N^*)

解析　因为n为正奇数，据数学归纳法证题步骤，第二步应先假设第k个正奇数也成立，本题即假设n＝2k－1正确，再推第(k＋1)个正奇数即n＝2k＋1正确．

答案　B

3．已知平面内有n条直线(n∈N^*)，设这n条直线最多将平面分割成f(n)个部分，则f(n＋1)等于

(　　)．

A．f(n)＋n－1                 B．f(n)＋n

C．f(n)＋n＋1                 D．f(n)＋n＋2

解析　要使这n条直线将平面所分割成的部分最多，则这n条直线中任何两条不平行，任何三条不共点．因为第n＋1条直线被原n条直线分成n＋1条线段或射线，这n＋1条线段或射线将它们所经过的平面区域都一分为二，故f(n＋1)比f(n)多了n＋1部分．

答案　C

4．已知S_n＝＋＋＋…＋，则S₁＝________，S₂＝________，S₃＝________，S₄＝________，猜想S_n＝________.

解析　分别将1,2,3,4代入观察猜想S_n＝.

答案　　　　　

5．用数学归纳法证明“当n为正偶数时xⁿ－yⁿ能被x＋y整除”第一步应验证n＝________时，命题成立；第二步归纳假设成立应写成________________．

解析　因为n为正偶数，故第一个值n＝2，第二步假设n取第k个正偶数成立，即n＝2k，故应假设成x^2k－y^2k能被x＋y整除．

答案　2　x^2k－y^2k能被x＋y整除

6．用数学归纳法证明：

1＋＋＋…＋＜2－(n≥2)．

证明：(1)当n＝2时，1＋＝＜2－＝，命题成立．

(2)假设当n＝k时命题成立，即1＋＋＋…＋＜2－，当n＝k＋1时，

1＋＋＋…＋＋＜2－＋＜2－＋＝2－＋－＝2－，命题成立．

由(1)、(2)知原不等式在n≥2时均成立．

7．用数学归纳法证明不等式＋＋…＋>(n∈N^*)的过程中，由n＝k递推到n＝k＋1时，下列说法正确的是

(　　)．

A．增加了一项

B．增加了两项和

C．增加了B中的两项，但又减少了一项

D．增加了A中的一项，但又减少了一项

解析　当n＝k时，不等式左边为＋＋…＋，

当n＝k＋1时，不等式左边为＋＋…＋＋＋.

答案　C

8．命题P(n)满足：若n＝k(k∈N^*)成立，则n＝k＋1成立，下面说法正确的是(　　)．

A．P(6)成立则P(5)成立

B．P(6)成立则P(4)成立

C．P(4)成立则P(6)成立

D．对所有正整数n，P(n)都成立

解析　由题意知，P(4)成立，则P(5)成立，若P(5)成立，则P(6)成立．所以P(4)成立，则P(6)成立．

答案　C

9．已知1＋2×3＋3×3²＋4×3³＋…＋n×3^n－1＝3ⁿ(na－b)＋c对一切n∈N^*都成立，则a、b、c的值为________．

解析　∵等式对一切n∈N^*均成立，∴n＝1,2,3时等式成立，即：

整理得解得a＝，b＝c＝.

答案　a＝，b＝c＝

10．数列{a_n}中，已知a₁＝2，a_n＋1＝(n∈N^*)，依次计算出a₂，a₃，a₄后，归纳、猜测得出a_n的表达式为________．

解析　a₁＝2，a₂＝，a₃＝，a₄＝，猜测a_n＝.

答案　a_n＝

11．求证：1＋≤1＋＋＋…＋≤＋n.

证明　(1)当n＝1时，f(1)＝1＋，原不等式成立；

(2)设n＝k(k∈N^*)时，原不等式成立

即1＋≤1＋＋＋…＋≤＋k成立，

当n＝k＋1时，

f(k＋1)＝f(k)＋＋＋…＋≥1＋＋＋＋…＋>1＋＋

＝1＋＋＝1＋，

f(k＋1)＝f(k)＋＋＋…＋≤＋k＋＋＋…＋<＋k＋

∴f(k＋1)<＋(k＋1)即n＝k＋1时，命题成立．

综合(1)、(2)可得：原命题对n∈N^*恒成立．

12．(创新拓展)数列{a_n}满足S_n＝2n－a_n，n∈N^*，先计算前4项后猜想a_n，并用数学归纳法证明．

证明　当n＝1时，S₁＝2－a₁，∴a₁＝1，

n＝2时，S₂＝a₁＋a₂＝4－a₂，∴a₂＝，

n＝3时，S₃＝a₁＋a₂＋a₃＝6－a₃，∴a₃＝，

n＝4时，S₄＝a₁＋a₂＋a₃＋a₄＝8－a₄，∴a₄＝.

∴猜想a_n＝.

用数学归纳法证明：①当n＝1时，a₁＝1，猜想成立，

②假设n＝k时猜想成立，即a_k＝成立．

那么，当n＝k＋1时，S_k＋1＝2(k＋1)－a_k＋1＝S_k＋a_k＋1＝2k－a_k＋a_k＋1，∴2a_k＋1＝2＋a_k＝2＋＝，

∴a_k＋1＝，即n＝k＋1时猜想成立．

由①②可知，对n∈N^*猜想均成立．