各种数学归纳法
1.5 归纳法原理与反归纳法
数学归纳法是中学教学中经常使用的方法.中学教材中的数学归纳法是这样叙述的:如果一个命题与自然数有关,命题对n=1正确;若假设此命题对n-1正确,就能推出命题对n也正确,则命题对所有自然数都正确.通俗的说法:命题对n=1正确,因而命题对n=2也正确,然后命题对n=3也正确,如此类推,命题对所有自然数都正确.对于中学生来说,这样形象地说明就足够了;但是毕竟自然数是无限的,因而上述描述是不够严格的,有了皮阿罗公理后,我们就能给出归纳法的严格证明.
定理1.19 如果某个命题T,它的叙述含有自然数,如果命题T对n=1是正确的,而且假定如果命题T对n的正确性就能推出命题T对n+1也正确,则命题T对一切自然数都成立.(第一数学归纳法)
证明 设M是使所讨论的例题T正确的自然数集合,则
(1)  .
.
设 ,则命题T对n正确,这时命题对
,则命题T对n正确,这时命题对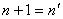 也正确,即
也正确,即
(2) 
所以由归纳公理D,M含有所有自然数,即命题T对所有自然数都成立.
下面我们给出一个应用数学归纳法的命题.
例1 求证

证明 (1)当n=1时,有

所以n=1,公式正确.
(2)假设当k=n时,公式正确,即

那么当k=n+1时,有
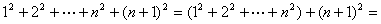


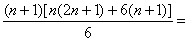



所以公式对n+1也正确.
在利用数学归纳法证明某些命题时,证明的过程往往归纳到n-1或n-2,而不仅仅是n-1,这时上述归纳法将失败,因而就有了第二数学归纳法.在叙述第二归纳法以前,我们先证明几个与自然数有关的命题.
命题1 若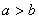 ,则
,则 .
.
证明 因为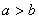
所以 

所以 
命题2 1是自然数中最小的一个.
证明 若 ,则
,则 有前元b,所以
有前元b,所以

命题3 若 ,则
,则 .
.
(即数 与
与 +1是邻接的两个数,中间没有其他自然数,不存在b,使得
+1是邻接的两个数,中间没有其他自然数,不存在b,使得 .)
.)
证明 若 ,则
,则 .
.
因为 ,所以
,所以 ,即
,即 .
.
由上述有关自然数大小的命题,我们得出下面定理,有时也称为最小数原理.
定理1.20 自然数的任何非空集合A含有一个最小数,即存在一个数 ,使得对集合A中任意数b,均有
,使得对集合A中任意数b,均有 .
.
证明 设M是这样的集合:
对于M中任意元素 ,对A中任意元素
,对A中任意元素 ,均有
,均有

则M是非空集合.
因为 ,由归纳公理(4)知,一定存在一个元素
,由归纳公理(4)知,一定存在一个元素 .
.
但 ,即
,即 ,
,
否则由 得M=N,这显然不可能.
得M=N,这显然不可能.
现在我们证明  .因为若
.因为若
 ,
,
则A中任意元素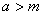

所以 ,与
,与 矛盾,所以m即为A中最小元素.
矛盾,所以m即为A中最小元素.
上述定理也称为最小数原则,有的作者把它当成公理,用它也可以证明数学归纳法,下面我们给出所谓第二数学归纳法.(第二数学归纳法)
定理1.21 对于一个与自然数有关的命题T,若
(1)当n=1时命题T正确;
(2)假设命题T对 正确,就能推出命题T对
正确,就能推出命题T对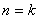 正确.
正确.
则命题T对一切自然数正确.
证明 如果命题T不是对所有自然数都成立,那么使命题不成立的自然数集合M就是非空集合,由定理1.20,M中含有一个最小数k,且 (∵k=1命题正确),所以对一切
(∵k=1命题正确),所以对一切 ,命题T成立,又由(2)推出命题T对k正确.结论矛盾.
,命题T成立,又由(2)推出命题T对k正确.结论矛盾.
下面我们给出两个只能应用第二数学归纳法而不能应用第一归纳法解题的例子.
例2 已知数列 ,有
,有
 且
且 
求证 .
.
证明 对n=1,有
所以命题对n=1正确.
假设命题对 正确,则
正确,则


所以命题对n=k正确.
由第二数学归纳法本题得证.
例3 已知任意自然数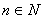 均有
均有
 (这里
(这里 )
)
求证
证明
(1)当n=1时,由 ,得
,得
所以命题对n=1正确.
(2)假设对 命题正确,这时
命题正确,这时
 ,
,
当n=k+1时,
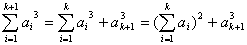 (1)
(1)
但是 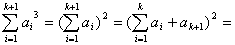
 (2)
(2)
又因为归纳假设对 命题正确,所以
命题正确,所以

所以 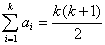
由(1)和(2)式得

消去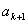 ,得
,得 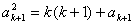
解得  舍去)
舍去)
所以命题对n=k+1也正确.
上边的两个例子,实际上例2命题归结到n-1和n-2,而例3则需要归结到1,2,…k,由此可见,第二数学归纳法的作用是不能由第一归纳法所替代的.
现在我们继续讲数学归纳法.当然,归纳并一定从n=1开始,例如例2数列的例子,也可以从某数k开始.数学归纳法还有许多变形,其中著名的有跳跃归纳法、双归纳法、反归纳法以及跷跷板归纳法等,下面我们就逐个介绍这些归纳法.
跳跃归纳法 若一个命题T对自然数 ,都是正确的;如果由假定命题T对自然数k正确,就能推出命题T对自然数
,都是正确的;如果由假定命题T对自然数k正确,就能推出命题T对自然数 正确.则命题对一切自然数都正确.
正确.则命题对一切自然数都正确.
证明 因为任意自然数

由于命题对一切 中的r都正确,所以命题对
中的r都正确,所以命题对 都正确,因而对一切n命题都正确.
都正确,因而对一切n命题都正确.
下面我们给出一个应用跳跃归纳法的一个例子.
例4 求证用面值3分和5分的邮票可支付任何n(n≥8)分邮资.
证明 显然当n=8,n=9,n=10时,可用3分和5分邮票构成上面邮资(n=8时,用一个3分邮票和一个5分邮票,n=9时,用3个3分邮票,n=10时,用2个5分邮票).
下面假定k=n时命题正确,这时对于k=n+3,命题也正确,因为n分可用3分与5分邮票构成,再加上一个3分邮票,就使 分邮资可用3分与5分邮票构成.由跳跃归纳法知命题对一切n≥8都成立.
分邮资可用3分与5分邮票构成.由跳跃归纳法知命题对一切n≥8都成立.
下面我们介绍双归纳法,所谓双归纳法是所设命题涉及两个独立的自然数对(m,n),而不是一个单独的自然数n.
双归纳法 若命题T与两个独立的自然数对m与n有关,
(1)若命题T对m=1与n=1是正确的;
(2)若从命题T对自然数对(m,n)正确就能推出该命题对自然数对(m+1,n)正确,和对自然数对(m,n+1)也正确.
则命题T对一切自然数对(m,n)都正确.
关于双归纳法的合理性证明我们不予说明,只给出一个例子.
例5 求证对任意自然数m与n均有

证明
(1)当 时,命题显然正确,即
时,命题显然正确,即

(2)设命题对自然数对m与n正确,即

这时 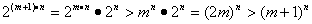
即命题对数对(m+1,n)正确;
另一方面

即命题对数对(m,n+1)也正确,由双归纳法知,命题对一切自然数对(m,n)都成立.
反归纳法 若一个与自然数有关的命题T,如果
(1)命题T对无穷多个自然数成立;
(2)假设命题T对n=k正确,就能推出命题T对n=k-1正确.则命题T对一切自然数都成立;
上述归纳法称为反归纳法,它的合理性我们做如下简短说明:
设M是使命题T不正确的自然数,如果M是非空集合,则M中存在最小数m,使得命题T对k=m不正确;由于命题对无穷多个自然数正确,所以存在一个 ,且命题T对
,且命题T对 正确;由于命题T对m不正确,所以命题对
正确;由于命题T对m不正确,所以命题对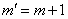 也不正确,否则由命题T对
也不正确,否则由命题T对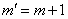 正确就推出命题T对m正确.矛盾!这样,命题T对m+2也不正确,经过
正确就推出命题T对m正确.矛盾!这样,命题T对m+2也不正确,经过 次递推后,可得命题T对
次递推后,可得命题T对 也不正确.这与已知矛盾,所以M是空集合.
也不正确.这与已知矛盾,所以M是空集合.
反归纳法又称倒推归纳法,法国数学家柯西(1789-1857)首次用它证明了n个数的算术平均值大于等于这n个数的几何平均值.
例6 求证n个正实数的算术平均值大于或等于这n个数的几何平均值,即

证明 当n=2时,

因此命题对n=2正确.
当n=4时,

因此命题对n=4正确
同理可推出命题对n=23=8,n=24,…,n=2s…都正确(s为任意自然数),所以命题对无穷多个自然数成立.
设命题对n=k正确,令

则

(容易证明上述是一个恒等式.)
由归纳假设命题对n=k正确,所以

所以 

即 
命题对n =k-1也正确,由反归纳法原理知,命题对一切自然数成立.
由于上述不等式是著名不等式,我们再给出几种证明:
前已证明,命题对n=2m时正确,设n<2m,令
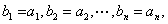

这时我们有


即 命题对n<2m正确
命题对n<2m正确
利用数学归纳法证明
不妨设n个数为 ,显然当n=1时命题正确.
,显然当n=1时命题正确.
设命题对 正确,令
正确,令

则 
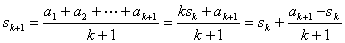
因为 ,所以
,所以


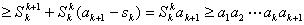
所以命题对n=k+1正确,由第一归纳法知,命题对一切自然数成立.
另一个有趣的证明是由马克罗林给出的,我们知道,若保持 和不变,以
和不变,以 分别代替
分别代替 和
和 ,这时两个数
,这时两个数 的和仍然是s,但两个数的积却增加了,即
的和仍然是s,但两个数的积却增加了,即

实际上两个数的算术平均值大于几何平均值,只有当两个数相等时才有等号成立.
现在我们变动诸数 ,但保持它们的和
,但保持它们的和 不变,这时乘积
不变,这时乘积

必然在 时取极大值.因为若
时取极大值.因为若 ,用
,用 分别代替
分别代替 与
与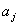 则
则 仍然不变,但它们的乘积
仍然不变,但它们的乘积

却增加了.而当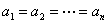 时,
时,

所以n个数的算术平均值大于等于几何平均值.
下面我们给出应用上述不等式的例子.
例7 在体积一定的圆柱形中,求其中表面积最小的一个(即在容积一定罐头中,求表面积最小的一个).
解 设圆柱的高为x,底圆半径为y,体积为V=常数,表面积为S,则
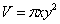

其中V为常数,欲求S的极小值.
已知 ,所以
,所以

即 
显然只有当 时,S取最小值.即当x=2y时,S值最小.
时,S取最小值.即当x=2y时,S值最小.
例8 求证在所有具有相同面积的凸四边形中,正方形的周长最短.
证明 用abcd表示四边形的四条边, 为a与b的夹角,
为a与b的夹角, 为c与d的夹角,如图1―1.用A表示四边形的面积,则
为c与d的夹角,如图1―1.用A表示四边形的面积,则

由(2)式得 

由(1)式得




其中
再利用半角公式 ,得
,得




所以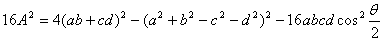
=
=
=
如令 四边形周长,得
四边形周长,得

因为 ,所以
,所以


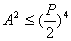
要使p最小(A为常数),只有当上式取等号时.即当
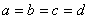 ,
,
且 °,这样的四边形只能是正方形.
°,这样的四边形只能是正方形.
最后,我们给出跷跷板归纳法.
有两个与自然数有关的命题An与Bn,若
(1)A1成立;
(2)假设Ak成立,就推出Bk成立,假设Bk成立就推出Ak+1成立.
则对一切自然数n, An与Bn都成立.

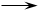 A1 B1
A1 B1
 A2 B2
A2 B2
 Ak Bk
Ak Bk

Ak+1
这里我们只给出一个例子说明上述归纳法.
例 已知

求证

证明 令  ,
,
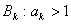
(1)当n=1时,

所以A1成立.
(2) 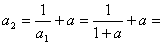

所以A2成立.
设Ak成立,则



即Bk成立.
若Bk成立,则

即Ak+1成立.由跷跷板归纳法知,一切An和Bn都成立.
练习1.5
(1)用数学归纳法证明 .
.
(2)求证
 .
.
(3)已知 ,且
,且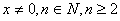 ,求证
,求证
 .
.
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
新课标高二数学归纳法(经典总结)
数学归纳法极限一第一数学归纳法一般地证明一个与自然数n有关的命题Pn有如下步骤1证明当n取第一个值n0时命题成立n0对于一般数列取…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
理科数学归纳法知识总结
理科数学归纳法知识总结一基本概念1运用数学归纳法证明命题要分两步第一步是归纳奠基或递推基础第二步是归纳递推或归纳假设两步缺一不可二…
-
数学归纳法教案(新)
教材背景:归纳是一种由特殊事例导出一般规律的思维方法.归纳推理分完全归纳推理与不完全归纳推理两种.不完全归纳推理只根据一类事物中的…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…