数学归纳法的历史
1 数学归纳法的历史
数学归纳法是数学中一种重要的证明方法, 用于证明与
自然数有关的命题。一旦涉及无穷,总会花费人们大量的时间
与精力,去研究它的真正意义。数学归纳法这个涉及“无穷”而
无法直观感觉的概念,自然也需要一个漫长的认识过程。
一般认为,归纳推理可以追溯到公元前 6 世纪的毕达哥
拉斯时代。毕达哥拉斯对点子数的讨论是相当精彩的。他由
有限个特殊情况而作出一般结论, 具有明显的推理过程,但
这些推理只是简单的列举,没有涉及归纳结果,因此是不完
全的归纳推理。完整的归纳推理,即数学归纳法的早期例证
是公元前 3 世纪欧几里得《几何原本》中对素数无限的证
明。其中已经蕴含着归纳步骤和传递步骤的推理。
16 世纪中叶,意大利数学家莫罗利科(F·Maurolycus)对
与自然数有关命题的证明进行了深入的研究。莫罗利科认
识到,对于一个与自然数有关的命题,为了检验其正确与否,
若采取逐一代入数进行检验的方法,那不是严格意义上的数
学证明, 要把所有的自然数都检验一遍是不可能做得到的,
因为自然数有无穷多个。那么对于这类问题该如何解决呢?
1575 年,莫罗利科在他的《算术》一书中,明确地提出了“递归
推理”这个思想方法。
法国数学家 B·帕斯卡(Pascal)对莫罗利科提出的递归推
理思想进行了提炼和发扬。在他的《论算术三角形》中首次使
用数学归纳法,并用其证明了“帕斯卡三角形”(二项展开式系数表,中国称为“贾宪三角性”或“杨辉三角形”)等命题。
“数学归纳法”这一名称最早见于英国数学家 A.德·摩
根 1838 年所著的《小百科全书》的引言中。德·摩根指出“这
和通常的归纳程序有极其相似之处”, 故赋予它“逐次归纳
法”的名称。由于这种方法主要应用于数学命题的证明,德·
摩根又提出了“数学归纳法”这个名称。
虽然数学归纳法早就被提出并广泛应用了,一直以来它
的逻辑基础都是不明确的。1889 年意大利数学家皮亚诺(G
Peano)建立了自然数的序数理论,将“后继”作为一种不加定
义的基本关系, 列举了自然数不加证明的五条基本性质,其
中归纳公理便为数学归纳法的逻辑基础。
至此,数学归纳法有了严格的逻辑基础,并逐渐演变为
一种常用的数学方法。
第二篇:数学归纳法的发展历程及应用
新乡学院
20##级毕业论文
论文题目:数学归纳法的发展历程及其应用
姓 名
学 号 10140302033
所在院系 数学与信息科学系
专业名称 数学教育
指导教师
指导教师职称 副教授
2013 年 04 月 20 日
目 录

内容摘要:本篇文章论述了数学归纳法的发展历程及其应用。数学归纳法的原理分析和探析及应用是本篇文章的主要内容。数学归纳法的发展几乎经历了整个数学的发展,从而从侧面给出数学发展的缩影。数学归纳法作为一种工具通常用在证明数学上的猜想,是解数学题最基本和最重要的方法之一,它在数学各个分支(解题、图论、中学数学等)都有着广泛的应用。数学归纳法是数学中一种重要的证明方法,也是中学数学一个非常重要的内容,用于证明与无穷的自然数集相关的命题。
关键词:数学归纳法 发展历程 应用 原理分析 中学数学 自然数集
Abstract:This article discusses the development history of mathe- matical induction. The principle analysis and analysis and application of mathematical induction is the main content of the paper. The develop- ment of mathematical induction almost witnessed the development of the whole history of mathematics, thus giving the epitome of mathematics from the side. Mathematical induction is one of the fundamental and the most important method of solving math problems, which has a wide range of applications in various branches of mathematics (problem solving, graph theory, secondary mathematics, ect). Mathematical induction is an important method of proof in mathematics and a very important content in middle school mathematics, which is used to prove propositions rel- ated to infinite natural number set.
Key words:Mathematical induction Development Application Prin-ciple analysis middle school mathematics Natural number set
1 数学归纳法的发展历程
数学归纳法是数学中一种重要的证明方法,也是中学数学一个非常重要的内容,用于证明与无穷的自数集相关的命题.但凡涉及无穷,总会花费数学家大量时间与精力,去理解并弄清它的真正意义.普通归纳法与自然数这一最古老的数学概念及“无穷”这个无法直观感觉的概念相结合的“数学归纳法”,自然也需要一个漫长的认识过程.
有限个数字、元素、对象的认识很容易,因为它们很直观,一个个“数”或一个个“考察”即可,当数字、元素、对象多到无数个,即“无限”或“无穷”个时,就不是这么简单数数、看看的事了,因这无穷多的对象是无法完全“摆”出来直观感受的,如果再带上一些复杂的关系,那就更加无法直观反映了.在“无穷”多个对象时,较简单的情形就是与自然数相关的“无穷”,比如用{P ( )}表示与自然数
)}表示与自然数 有关的无穷多的数字、元素、对象或性质、命题等.为了“数”清这无穷多的对象,或“看”清摆不出来的对象是否也带有看得到的对象所具有的复杂关系,那只能用“归纳”的办法去合理地“猜”,这就是普通“归纳法” 的作用,是人类认识未知的一个普遍有效的方法,它是通过少数几个对象所显现的特征,根据后面对象与这少数对象在看得到、感觉得了的“相似”关系中,合理推测这些对象特征的办法.这时,也许你运气好恰好“猜”对了,也许没那么好的运气,一而再再而三地猜错,即使你猜对了,对数学家而言也不敢轻易恭维,因为他们需要的是“准确”的计数或“清晰” 地看到性质,也就是说,必须对你的猜测给予严格的证明才能认可.
有关的无穷多的数字、元素、对象或性质、命题等.为了“数”清这无穷多的对象,或“看”清摆不出来的对象是否也带有看得到的对象所具有的复杂关系,那只能用“归纳”的办法去合理地“猜”,这就是普通“归纳法” 的作用,是人类认识未知的一个普遍有效的方法,它是通过少数几个对象所显现的特征,根据后面对象与这少数对象在看得到、感觉得了的“相似”关系中,合理推测这些对象特征的办法.这时,也许你运气好恰好“猜”对了,也许没那么好的运气,一而再再而三地猜错,即使你猜对了,对数学家而言也不敢轻易恭维,因为他们需要的是“准确”的计数或“清晰” 地看到性质,也就是说,必须对你的猜测给予严格的证明才能认可.
如此一来,如何“准确”数、“清晰”看对象或其性质,就成了数学家伤脑筋的一个问题,这一“数”就数了两千多年.从普通不严密的“归纳法”发展到精确的“数学归纳法”,再到更一般的“超穷归纳法”、“连续归纳法”.
1.1 数学归纳法的起源
追根溯源,数学归纳法可以在印度和古希腊时代的著作中找到丝缕痕迹,例如,印度婆什迦罗(Bhāskara,1114~约1185)的“循环方法”和欧几里得素数无限的证明中都可以找到这种踪迹.欧几里得《几何原本》第九卷命题20为:质数比任何指定数目都要多(注:质数也称为素数),即:素数无穷.欧几里得对这个命题的证法是经典的.他假定素数是有限的,不妨设这有限的 个素数为
个素数为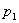 、
、 、… 、
、… 、 .然后作自然数
.然后作自然数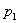 ﹒
﹒ …
… +1,并证明还存在新的素数,从而得到矛盾.因为若所作的数是素数,则它比全部给出的
+1,并证明还存在新的素数,从而得到矛盾.因为若所作的数是素数,则它比全部给出的 个素数都要大,因此是一个新的素数,这与假设有
个素数都要大,因此是一个新的素数,这与假设有 个素数矛盾;又若它不是素数,它必能被一素数整除,但它被已知全部的
个素数矛盾;又若它不是素数,它必能被一素数整除,但它被已知全部的 个素数
个素数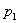 、
、 、… 、
、… 、 除都有余数1,故整除
除都有余数1,故整除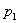 ﹒
﹒ …
… +1的素数必定是这
+1的素数必定是这 个素数以外的新的素数,从而又与假设有
个素数以外的新的素数,从而又与假设有 个素数的条件矛盾.
个素数的条件矛盾.
欧几里得素数无穷命题即是说,素数的个数与自然数的个数一样多.上述证明可以这样 翻译,首先,至少有一个素数存在,因为2就是素数,这一点在欧几里得的证明中没有指明;此外,上面欧几里得的证明表明,假如有 个素数,那么就必定有
个素数,那么就必定有 个素数存在.也就是按现代数学归纳法的要求,证明了从
个素数存在.也就是按现代数学归纳法的要求,证明了从 到
到 的递推关系,即完成了数学归纳法证明的关键性一步.但欧几里得没有使用任何明显的术语与现在的推理格式,因此,我们只能认为它蕴涵了现代数学归纳法的痕迹.
的递推关系,即完成了数学归纳法证明的关键性一步.但欧几里得没有使用任何明显的术语与现在的推理格式,因此,我们只能认为它蕴涵了现代数学归纳法的痕迹.
1.2 数学归纳法的发展推广
1.2.1数学归纳法的发展
直到十七世纪后,在数学归纳法有了明晰的框架后,各种形式的数学归纳法逐步得到发展,具体使用中的各种变异形式,如奠基步骤中的起始命题证明、归纳步骤中的跳跃台阶设置等都作了相应推广,发展出了最小数原理、第一和第二数学归纳法、反向归纳法、递减归纳法、螺旋归纳法、双重甚至多重归纳法等各种形式的数学归纳法.由于分析算术化的需要,数的理论也得到了充分发展,并最终将整个分析建基于自然数之上,至1889年意大利数学家C·皮亚诺(C·Peano,1858~1932,意大利)发表 算术原理新方法,给出自然数的公里体系,不仅使全部微积分理论根基于此,也使数学归纳法有了一个准确、合理的理论基础.
Peano自然数公理系统:
Ⅰ.1是一个自然数;
Ⅱ.1不是任何其他自然数的后继;
Ⅲ.每个自然数的后继是自然数;
Ⅳ.若两个自然数的后继相等, 则这两个自然数也相等;
Ⅴ. 若M是由一些自然数所组成的集合,而且1属于 M,且当任一自然数 属于M 时,
属于M 时, 的后继也属于M,则 M 就包含了全部自然数.
的后继也属于M,则 M 就包含了全部自然数.
其中公理V被称为归纳公理,是数学归纳法的逻辑基础.
几乎同时,在分析算术化的过程中,对“无穷”概念作出了深刻的分析,扫除了微积分发展中的主要障碍,并对分析中的“不健康”点(不连续点、不收敛点等)逐渐有了深刻认识,为最终建立实分析奠定了基础.在对“例外”的考虑中,康托尔是独具慧眼的数学家,以此为起点,康托尔在 1897年建立了集合论基础,并对自然数作了深入、细致的研究,发明了超穷数,建立了超穷序数与超穷基数理论,并论述了良序集的特别理论,在此基础上将数学归纳法扩展为超穷归纳法.我们熟悉的归纳公理用集合论的语言可表述为:
设S是自然数集合N的一个子集,如果:(1)1是 S的元素;(2)从 是S的元素可推出
是S的元素可推出 + 1是S的元素. 那么,(3)S= N.
+ 1是S的元素. 那么,(3)S= N.
对于良序化的集合也有类似的性质:
设 A 是良序化的集合,S 是 A 的一个子集,如果(1)A 的最小元素是 S的元素;(2) 是A 的元素,而从所有在A中比
是A 的元素,而从所有在A中比 小的元素是S的元素可推出
小的元素是S的元素可推出 也是S的元素. 那么,(3)S= A.
也是S的元素. 那么,(3)S= A.
由彼此相似的良序集确定的数称为序数, 对于这样的良序集和序数相应的有下列超穷归纳法(有些教材或专业书直接将上述命题称为超穷归纳法):
超穷归纳法 设 是序数
是序数 的一个命题,并且满足:如果任给
的一个命题,并且满足:如果任给 <
< ,
, 都成立,则
都成立,则 成立.那么,任给序数
成立.那么,任给序数 ,
, 都成立.
都成立.
因为没有序数比0小,所以“任给 <
< ,
, 都成立”总是真的,因此上述归纳法定理的条件中蕴涵着
都成立”总是真的,因此上述归纳法定理的条件中蕴涵着 成立.应用时,有时需要特别证明
成立.应用时,有时需要特别证明 成立.如若讨论的是大于等于某个序数
成立.如若讨论的是大于等于某个序数 的所有序数的性质,这时,与应用普通数学归纳法一样,需要对超穷归纳法条件需要稍加改动.上述条件改为:
的所有序数的性质,这时,与应用普通数学归纳法一样,需要对超穷归纳法条件需要稍加改动.上述条件改为:
如果任给
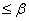 <
< ,
, 都成立,则
都成立,则 成立.
成立.
易知,数学归纳法是超穷归纳法的特殊形式,但从数学归纳法不能推出超穷归纳法,因为自然数集只是特殊的良序集,而普通的数学归纳法无法跨越无穷达到“超穷”.
数学归纳法和超限归纳法是对“离散”的无穷数集作出判断的严格的数学方法.对于连续情形,直到上世纪80年代才发现有一个十分简单而又便于掌握与应用的关于实数的归纳法,称为连续归纳原理或连续归纳法:
设 P ( )为关于实数
)为关于实数 的一个命题,如果
的一个命题,如果
(i)有某个实数 ,使得对一切实数
,使得对一切实数 <
< ,有 P (
,有 P ( )成立;
)成立;
(ii)若对一切实数 <
<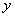 有 P (
有 P ( )成立,则有
)成立,则有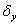 > 0,使 P (
> 0,使 P ( )对一切实数
)对一切实数 <
<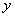 +
+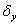 成立.
成立.
那么,(iii)对一切实数 有P(
有P( )成立.
)成立.
连续归纳法与数学归纳法或超穷归纳法形式极为相似,某种程度上表明离散的自然数集或良序集与连续的实数集在一定条件下的统一性.连续归纳法可以用来刻画实数系统的连续性公理,并推出一系列关于实数的命题,以及微积分中涉及连续的所有命题,连续归纳法的发现使有关实数的命题变得简单而易于掌握.
至此,“归纳法”完成了较全面的、数学化的发展,“数学归纳法”在有限与无限之间架起了一座安全的桥梁.随着数学对象的进一步扩展,严格、准确的“归纳法”表达形式或许还会有更进一步的发展,因为数学概念的本身就是随着数学的整体发展以及人类认识的不断深化而逐步深入地修改、完善的,文献[8]用集合论的基本概念、现代数学的术语包括代数结构的语言与逻辑手段阐述数学归纳法,以表明数学归纳法的现代建构及其应用.
综上所述,“归纳法”的精确化、成熟化几乎伴随了整个数学发展、成熟的历史, 从古代印度数学和古希腊欧几里得《几何原本》至二十世纪下半叶连续归纳法的发现.
1.2.2数学归纳法的推广
数学归纳法是一个非常常用的数学工具,它在论证有关自然数的命题时十分有用.本文中试图将通常适用于自然数系的数学归纳法推广到下有界整数集{ |
|
 Z,
Z,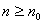 } 与上有界整数集{
} 与上有界整数集{ |
|
 Z,
Z,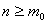 }及全体整数集Z.作为应用,证明关于二元命题{
}及全体整数集Z.作为应用,证明关于二元命题{ }|
}|
 Z的数学归纳法.
Z的数学归纳法.
定理1 设{ }
} 是与整数
是与整数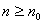 ,有关的一列命题且满足以下条件:
,有关的一列命题且满足以下条件:
(1)P(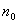 )成立;
)成立;
(2) 成立
成立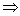 P(
P( +1)成立,则对任一整数
+1)成立,则对任一整数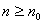 ,命题P(
,命题P( )都成立.
)都成立.
证明 定义 Q( ) = P(
) = P( +
+ 1),则{Q(
1),则{Q( )}|
)}| ∈N 是与自然数
∈N 是与自然数 ∈N 有关的一列命题且满足以下条件:
∈N 有关的一列命题且满足以下条件:
(1)Q(1)成立;
(2)Q( ) 成立
) 成立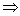 Q(
Q( +1)成立.
+1)成立.
因此,由通常数学归纳法可知:
 ∈N,命题Q(
∈N,命题Q( )成立,从而
)成立,从而 ∈Z且
∈Z且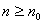 ,命题P(
,命题P( ) 都成立.
) 都成立.
推论1 设{ P( ) }
) }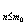 是与整数
是与整数 有关的一列命题且满足以下条件:
有关的一列命题且满足以下条件:
(1)P( ) 成立;
) 成立;
(2)P( )成立
)成立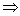 P(
P( 1)成立,则对任一整数
1)成立,则对任一整数 ,命题P(
,命题P( )都成立.
)都成立.
证明 设Q( ) = P(
) = P( ),
),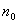 =
= ,则{Q (
,则{Q ( )}
)} 是与整数
是与整数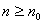 有关的一列命题且满足以下条件:
有关的一列命题且满足以下条件:
(1)Q(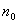 )成立:
)成立:
(2)Q( )成立
)成立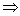 Q(
Q( +1)成立.
+1)成立.
于是,由定理 1知:对任一整数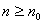 ,命题Q(
,命题Q( )都成立.因此,对任一整数
)都成立.因此,对任一整数 ,命题P(
,命题P( )都成立.
)都成立.
定理2 设{P( )}|
)}| ∈Z是与整数
∈Z是与整数 ∈Z有关的一列命题且满足以下条件:
∈Z有关的一列命题且满足以下条件:
(1)对某一整数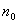 ,P(
,P(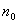 ) 成立;
) 成立;
(2)P( )成立P(
)成立P( ±1)成立,则
±1)成立,则 ∈Z,命题P(
∈Z,命题P( )都成立.
)都成立.
证明 由定理1知: ∈Z且
∈Z且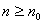 ,命题P (
,命题P ( )成立.再由推论1知:
)成立.再由推论1知: ∈Z,且
∈Z,且 ,命题P(
,命题P( )都成立. 故
)都成立. 故 ∈Z,命题 P(
∈Z,命题 P( ) 都成立.
) 都成立.
定理3 设{ P( ,
, ) }|
) }| ,
, ∈Z是与整数
∈Z是与整数 ,
, ∈Z有关的一列命题且满足以下条件:
∈Z有关的一列命题且满足以下条件:
(1)对某一对整数 ,
,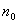 ,P(
,P( ,
,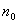 )成立;
)成立;
(2)P ( ,
, ) 成立P(
) 成立P( ,
, ±1),P
±1),P  ±1,
±1, )都成立.则对任一整数对(
)都成立.则对任一整数对( ,
, )∈Z
)∈Z =Z×Z,命题P(
=Z×Z,命题P( ,
, )都成立.
)都成立.
证明 对任一整数 ∈Z,考虑命题:
∈Z,考虑命题:
Q( ):对任一整数
):对任一整数 ∈Z,P (
∈Z,P ( ,
, ) 成立.由于命题P(
) 成立.由于命题P( ,
,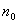 )成立,且P(
)成立,且P( ,
, )成立
)成立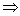 P(
P( ,
, ±1)成立,从而由定理2知:
±1)成立,从而由定理2知: ∈Z,命题P(
∈Z,命题P( ,
, )都成立.这说明,命题Q(
)都成立.这说明,命题Q( )成立.设命题Q(
)成立.设命题Q( )成立即
)成立即 ∈Z,命题P(
∈Z,命题P( ,
, )都成立.从而由条件(2)知:
)都成立.从而由条件(2)知: ∈Z,命题P(
∈Z,命题P( ±1,
±1, )都成立,即命题Q(
)都成立,即命题Q( ±1)成立,这就证明了:
±1)成立,这就证明了:
(1)命题Q( )成立;
)成立;
(2)设命题Q( )成立,则命题Q(
)成立,则命题Q( ±1) 成立.
±1) 成立.
因而,由定理2知:
 ∈Z,命题Q(
∈Z,命题Q( )都成立,即(
)都成立,即( ,
, )∈Z
)∈Z = Z×Z,命题P(
= Z×Z,命题P( ,
, )都成立.
)都成立.
类似于定理3之证明,不难证明以下更一般的数学归纳法:
定理4 设 P(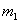 ,
, ,…,
,…, ) 是与整数组(
) 是与整数组(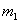 ,
, ,…,
,…, )∈Z
)∈Z
有关的命题且满足条件:
(1)对某一组整数(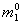 ,
, ,…,
,…, ),命题 P (
),命题 P (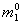 ,
, ,…,
,…, ) 成立;
) 成立;
(2)P(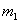 ,
, ,…,
,…, )成立 P (
)成立 P (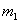
 ,
, ,…,
,…, ) ,P(
) ,P(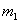
 ,
, ,…,
,…, ),…,P(
),…,P(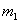
 ,
, ,…,
,…, )都成立,则对任一组整数(
)都成立,则对任一组整数(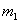 ,
, ,…,
,…, )∈Z
)∈Z ,命题 P(
,命题 P(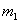 ,
, ,…,
,…, )都成立.
)都成立.
2 数学归纳法的应用
数学归纳法是一种证明与自然数n有关的数学命题的重要方法,也是一种常用的不可缺少的推理论证方法,没有它,在图论中很多与自然数有关的命题难以证明;同时对于与自然数有关的命题,把n所取的无穷多个值一一加以验证是不可能的,用不完全归纳法验证其中一部分又很不可靠,数学归纳法则是一种用有限步骤证明与自然数有关的命题的可靠方法,其思维方式对于开发学生的智力有重要价值.在图论学习中,掌握并应用好这一方法有十分重要的意义.
本篇文章对数学归纳法的应用我先从其原理入手进行分析,逐步对数学归纳法的逻辑原理、原理分析、理论依据与适用范围和基本形式进行介绍分析,最后再对其应用进行介绍.
2.1 数学归纳法的原理分析
2.1.1数学归纳法的逻辑原理
数学归纳法是一种证明与自然数n有关的数学命题的重要方法.我们首先看一个简单的、人们熟悉的归纳集合,即自然数集N={0,1,…}.要确定N,可先给出一个特殊的元素0,称为初始元,它是产生N 的基础.然后再给出一个由自然数产生自然的运算,即一元后继运算n′(=n+1).这个运算作用在初始元0上得到1,再作用在1上得到2,把这个过程一直继续下去,就可以依次把所有自然数产生出来.这个后继运算n′有一个性质,即当n∈N时,则n′∈N。令P是自然数的一个公共性质,并令P(n) 是一个命题,表示自然数n有性质P.现在假设命题:(1)P(0);(2)所有n,如果P(n)成立,则P(n′)成立,那么可得:(3) 则所有n,P(n).这就是通常所说的数学归纳法原理,用公式可表示为:P(0)∧ n(n∈N∧(p(n)→P(n′))) →
n(n∈N∧(p(n)→P(n′))) → n(n∈N∧p(n))或者表示为:
n(n∈N∧p(n))或者表示为: n(n∈N ∧p(m)∧(m<n))→P(n)→
n(n∈N ∧p(m)∧(m<n))→P(n)→ n(n∈N∧p(n))它是数学归纳法(简称归纳证明)的基础.根据该原理,我们可在有限的步骤内,证明自然数集中无限的元素都有某性质,即只要证明上述命题(1)和(2),我们就归纳地证明了命题(3).
n(n∈N∧p(n))它是数学归纳法(简称归纳证明)的基础.根据该原理,我们可在有限的步骤内,证明自然数集中无限的元素都有某性质,即只要证明上述命题(1)和(2),我们就归纳地证明了命题(3).
2.1.2数学归纳法的原理
自然科学中的经验归纳法,是从某一现象的一系列特定的观察出发,归纳出支配该现象所有情况的一般规律,而数学归纳法则是迥然不同的另种手段,它用来证实有关无限序列(第一个,第二个,第三个,…等等,没有一个情况例外)的数学定理的正确性.
数学归纳法原理:假设我们希望证明一系列无限个数学命题 A ,A
,A ,A
,A ,…,它们合在一起便构成一般的命题A.如果
,…,它们合在一起便构成一般的命题A.如果
a)通过某种数学论证可以证明,对于任一整数r,如果命题A 已知为真,则命题A
已知为真,则命题A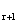 随之亦真;
随之亦真;
b)第一个命题A 已知为真,那么序列中所有命题必都为真,从而A得证.
已知为真,那么序列中所有命题必都为真,从而A得证.
数学归纳法的原理是奠基在下属事实的基础上:在任一整数 r 之后接着便有下一个 r+1,从而从整数1出发,通过有限多次这种步骤,便能达到任意选定的整数n.
推广后的数学归纳法原理:假设给定一系列命题 A ,A
,A ,A
,A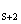 ,…,其中S是某正整数,如果
,…,其中S是某正整数,如果
a) 对于每个r≥s,A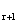 的正确性可以从A
的正确性可以从A 的正确性导出;
的正确性导出;
b)A 已知为真,则所有命题A
已知为真,则所有命题A ,A
,A ,A
,A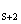 ,…均为真;换句话说,对于所有的n≥s,A
,…均为真;换句话说,对于所有的n≥s,A 为真.
为真.
我们再次强调指出,在自然科学中,数学归纳法原理与经验归纳法是完全不同的,一般的定律如果被证实了任意有限次,那么不论次数多么多,甚至至今尚未发现例外,都不能说该定律在严格的数学意义下被证明了,这种定律只能算作十分合理的假设,它容易为未来的经验结果所修正.在数学中,一条定律或一个定理所谓被证明了,指它是从若干作为真理接受的假设出发得到的逻辑推论.人们考察一个定理,如果它在许多实例中是正确的,那么就可猜想定理在普遍意义下将是真的;然后人们尝试用数学归纳法以证明之.如果尝试成功,定理被证明为真;如果尝试失败,则定理的真伪未定,有待以后用其他方法予以证明或者推翻.因此在应用数学归纳法原理是要牢记 a)和 b)必须真正的满足.
2.1.3数学归纳法的原理分析
(1)数学归纳法的具体表现形式
归纳法分为完全归纳法和不完全归纳法,而数学归纳法属于完全归纳法,它又分为有限数学归纳法和超限数学归纳法,对于后者,在实变函数论中会学到;前者有两种不同的形式,它们分别叙述为:
第一数学归纳法:如果性质P(n)在n=1时成立,而且在假设了n=k时性质P(k)成立后,可以推出在n=k+1时性质P(k+1)也成立,那么我们可以断定性质P(n)对一切自然数n都成立.
第二数学归纳法:如果性质P(n)在n=1时成立,而且在假设了对所有小于或等于 k 的自然数n性质P(n)都成立后,可以推出在n=k+1时性质P(k+1)也成立,那么性质P(n)对一切自然数n都成立.
下面我们来看第一数学归纳法和第二数学归纳法之间的关系,可以用一个定理说明.
定理 第一数学归纳法和第二数学归纳法等价.
证明 假设性质 P(n)在 n=1 时成立,于是化为证明:由P(k)成立,则可以推出 P(k+1)成立的充分必要条件为由 P(n)(其中 n≤k)成立,可以推出 P(k+1)成立.
必要性:由已知 由 P(k)成立,则可以推出 P(k+1)成立,假设 n≤k 时 P(n)成立,特别P(k)成立,所以 P(k+1)成立.得证.
充分性:(反证法证明)由已知n≤k时P(n)成立,可以推出 P(k+1)成立,于是,由 P(k )成立推不出 P(k
)成立推不出 P(k +1)成立的所有自然数k
+1)成立的所有自然数k 构成一非空子集,记m为该子集的最小自然数.所以,对任一自然数 n,只要 n<m,那么由 P(n)成立可以推出 p(n+1)成立.特别,由 P(1)成立可知 P(2)成立,由 P(m-1)成立可知 P(m) .已知 P(1)成立,因此 P(1) 、P(2)、…、 P(m)都成立,然而由此可知 P(m+1)成立,所以从 P(m)成立推出了 P(m+1)成立;另一方面,由 m 的选取可知,由 P(m)成立推不出 P(m+1)成立,这就导出矛盾,得证.对于数学归纳法的特殊形式就简单介绍到这里.当然还有许多形式更为复杂的归纳法,如反向归纳法、往返归纳法、超限归纳法等等.
构成一非空子集,记m为该子集的最小自然数.所以,对任一自然数 n,只要 n<m,那么由 P(n)成立可以推出 p(n+1)成立.特别,由 P(1)成立可知 P(2)成立,由 P(m-1)成立可知 P(m) .已知 P(1)成立,因此 P(1) 、P(2)、…、 P(m)都成立,然而由此可知 P(m+1)成立,所以从 P(m)成立推出了 P(m+1)成立;另一方面,由 m 的选取可知,由 P(m)成立推不出 P(m+1)成立,这就导出矛盾,得证.对于数学归纳法的特殊形式就简单介绍到这里.当然还有许多形式更为复杂的归纳法,如反向归纳法、往返归纳法、超限归纳法等等.
(2)数学归纳法的原理分析
(Ⅰ)第一数学归纳法理论基础及证明
第一数学归纳法的理论基础为自然数的序数理论,是由意大利数学家 Peano 于1889年在他的著作《算数原理新方法》中提出.该理论用公理化的方法从顺序的角度揭示了自然数的意义,即我们所说的自然数 1、2、3……理解为第1个、第 2 个、第 3 个……下面用定义的方式给出这个公理的内容.
定义: 一个非空集合 N 的元素叫做自然数,如果 N 的元素之间有一个基本关系“后续”(用符号'来表示),并满足下列公理:
(1) 1 N,对
N,对 a
a N,a'≠1;
N,a'≠1;
(2) 对任何a N 有唯一的后继元素a'.
N 有唯一的后继元素a'.
(3)1以外的任何元素只能是一个元素的后继元素,即1不排在任何自然数后面
(4) 归纳公理:若 M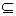 N 且
N 且
① 1 M
M
② a M
M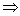 a
a 'N 则M
'N 则M N(N自然数集)
N(N自然数集)
定义中的一组公理叫 Peano 公理.它完整地刻画了自然数列,而其中的公理(4)即归纳公理可推出第一数学归纳法.
第一数学归纳法设P(n)是一个与自然数有关的命题,如果:
P(1)成立
假设 P(k) 成立 则 P(k +1)成立
那么对任意自然数P(n)都成立
证明:设M是由满足P(n)的自然数组成的集合则M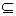 N
N
∵ P(1)成立,则1 M
M
又∵ 假设P(k)成立 则P(k+1)成立 即 k M
M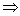 k +1
k +1 M
M
即 k M
M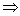 k'
k' M 由归纳公理 M = N
M 由归纳公理 M = N
M 为自然数集即P(n)对任意自然数都成立.
从上述证明过程可以看出第一数学归纳法的理论依据为归纳公理.
(Ⅱ)第二数学归纳法理论基础及证明
第二数学归纳法也属于数学归纳法.它的理论依据为最小数原理,而最小数原理实际上也是归纳公理得出的.最小数原理: 自然数集的任一非空子集中必有一个最小数.
证明:设A为N的任一非空子集,由皮亚诺公理(3)假设 n N 且 n≠1 则 n 必为某一自然数 m 的后续.
N 且 n≠1 则 n 必为某一自然数 m 的后续.
∴ n = m' = m + 1>1
∴ 自然数集N有最小数1
∴ 当1 A,A有最小数1
A,A有最小数1
当1 A 时,假设 A 没有最小数
A 时,假设 A 没有最小数
构造集合T={ xx N 且对
N 且对 a
a A x<a}
A x<a}
则 1 T
T
假设 n T 若 n +1
T 若 n +1 A 则 n +1 为 A 中的最小数与假设矛盾.
A 则 n +1 为 A 中的最小数与假设矛盾.
∴ n +1 T
T
那么1 T,n
T,n T时n+1
T时n+1 T由归纳公理T=N,则A=
T由归纳公理T=N,则A=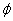 与A为非空集矛盾.
与A为非空集矛盾.
∴ N 的任一非空子集中必有一个最小数.
以上是用归纳公理对最小数原理作证明.
下面用最小数原理对第二数学归纳法做一个证明.
第二数学归纳法:设P(n)是一个与自然数有关的命题
若下列两个条件成立:(1)P(1)成立;(2)假设P(n)对于所有满足 l<k 成立,则 P(k)成立,那么P(n)对所有自然数成立.
证明:设M为满足P(n)成立的所有自然n的集合,设T=N—M,假设T≠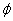 根据最小数原理T有最小数
根据最小数原理T有最小数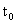 .由条件(1):P(1)成立,则1
.由条件(1):P(1)成立,则1 M.
M.
∴ 
∴ 1、2、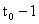
 M
M
又由条件(2)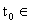 T 矛盾
T 矛盾
∴ 
∴ M=N
∴ P(n)对任意自然数成立.
2.2 数学归纳法的探析及应用
数学归纳法是数学中最基本也是最重要的证明方法之一,在数学各个分支里都有广泛应用.该法的实质在于:将一个无法(或很难) 穷尽验证的命题转化为证明两个普通命题“P (1) 为真”和“P (k)为真则P (k+1)为真”,从而达到证明目的.该部分讨论的是数学归纳法的理论依据、适用范围、基本形式、证题技巧和数学归纳法的应用.
2.2.1数学归纳法的理论依据
数学归纳法是用以严格论证与自然数有关命题的正确性,与自然数有关的命P(n)一般是由无穷多个命P(1),P(2),P(3),P(n) 所组成,采用逐个论证的方法是不可能的.数学归纳法的实质在于将一个无法或很难穷尽验证的命题转化为两个普通的命题“P(1)为真”和“P(k)为真则P(k+1) 为真”,从而达到证明的目的,是从有限范围内的结论出发,利用自然数的“后续”特征和逻辑中的“蕴含”关系,得到无限范围内无可辩驳、不可怀疑的正确结论.
数学归纳法的理论依据来源于揭示自然数根本性质的皮亚诺定理,自然数集是满足下述一组公理的集合.
(1) 1是一个自然数.
(2) 对于N的每一个自然数n,都可以在N找到一个后续自然数n+1.
(3) 对于任何自然数n,n+1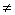 1,即没有1为“后续”数的自然数.
1,即没有1为“后续”数的自然数.
(4) 任何两个自然数n与m,若m+1=n+1,则n=m.
(5) N的任一子集若满足性质: (a) 1 S,(b) n
S,(b) n S,可推出n+1
S,可推出n+1 S,则S=N.
S,则S=N.
“后续”关系是自然数的重要特征,即每个自然数有且仅有一个“后续”,这是数学归纳法的第二步归纳递推的依据.可见皮亚诺公理的第五条正是数学归纳法的根据,因此第五条公理也称作数学归纳法原理.这种推理方法,可说是数学中的“多米诺”现象,如果不具有一定数学和逻辑素养,是不可能相信和理解的.它体现了人类理性思维“从有限认识到无限”所闪烁的智慧之光.
2.2.2数学归纳法的适用范围
数学归纳法的证明一般实用于自然数集的某一无限子集(即其最小的自然数为n)有关的命题P(n)的证明,但有些命题中n可取整数,也可用数学归纳法,而且归纳推理的思想对于关于自然数集的某一有限子集的命题的证明也是可以借鉴的.如高等数学中“有限个”具有极限的函数的和、差、积、商(分母不为0)、幂的极限仍存在且等于它们各自极限的和、差、积、商、幂等, 这里的“有限个”只对于“自然数的有限子集”,也可利用数学归纳法的思路予以推证,不要在最后下结论:对所有自然数都成立.
2.2.3数学归纳法的证题技巧
(1)“起点后移”或“起点前移”,有些关于自然数n的命题P(n).验证P(1)比较困难,或者 P(1),P (2), P(r – 1)不能统一到归纳的过程中去,这时可考虑到将起点前移至P(0)(如果有意义),或后移到P(r)(这时P(1),P(2),P(r – 1)应另行证明).
(2)加大“跨度”,这时定义 M = { n,n + r,n +2r,…,n+ mr}(n,r,m∈N)上的命题.在采用数学归纳法时,应考虑加大“跨度”的方法,即第一步验证 P(n),第二步假设P(k)(k∈M)成立,推出 P(n + r)成立.
2.2.4数学归纳法的应用
为了体现数学归纳法在数学中的地位,下面举例来说明其应用.数学归纳法的应用.
(1)第一数学归纳法的应用
例1 某生产队科学实验小组决定研究n(n≥2)种害虫之间的关系,然后想法消灭它们,经实验,他们发现,其中任意两种总有一种可吞食另一种.试证明可把此几种害虫排成一行,使得前一种可吞食后一种.
证明(1)n=2 时,命题显然成立.
(2)设 n=k 时( 2),结论成立.我们不妨以
2),结论成立.我们不妨以 (i=1,2,… ,k)表示第i种害虫,记这时可将它们排成
(i=1,2,… ,k)表示第i种害虫,记这时可将它们排成 ,
, ,…
,…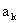 ,其中前一种可吞食后一种.用(
,其中前一种可吞食后一种.用(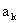 >
> 表示可吞食
表示可吞食 )
)
下面考虑 n=k+1 时的情形,即在上面情形里加进一种害虫
(当然,我们还可以将k+1种害虫分为两组,一组k种,一组一种,由归纳假设第一组k种可排成 ,
, ,…
,…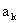 ,使前一种可吞食后一种,再将第二组的一种记为
,使前一种可吞食后一种,再将第二组的一种记为 加入),将有下面两种情形:
加入),将有下面两种情形:
①若 >
> ,则可将
,则可将 置
置 前,则有
前,则有 >
> >
> >
> 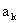 .命题为真.
.命题为真.
②若 >
> ,再将
,再将 与
与 放在一起试验,若
放在一起试验,若 >
> ,可将
,可将 置
置 后
后 前即可,这时有
前即可,这时有 >
> >
> >
> 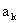 ,命题为真.否则可重复往下试验,经过有限次(
,命题为真.否则可重复往下试验,经过有限次( k次),必有下列情形之一:
k次),必有下列情形之一: >
> >
> ,问题解决.
,问题解决.
否则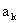 >
> ,则可置 ak+1于 ak之后.此时有
,则可置 ak+1于 ak之后.此时有 >
> >
>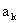 >
>  ,命题亦成立.
,命题亦成立.
综上,命题对k+1成立,从而对任意自然数(n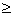 2)成立.
2)成立.
2 第二数学归纳法的应用
例2 计算行列式

分析:该行列式如果直接计算很困难,也很难发现什么规律,但是如果先依最后一行展开,则可得递推公式:
 2
2 (1)而
(1)而 时
时
 ,
, 时,
时, ,
,
 2
2 ,由此可猜想
,由此可猜想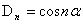 .
.
下面用第二数学归纳法证明
证明(1)当 时,
时,
 ,猜想成立.
,猜想成立.
(2)假设 时,
时, ,当
,当 时,由式(1),有D
时,由式(1),有D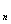 =
=




 ,故
,故 时,有
时,有 ,归纳法完成,故对一切 n
,归纳法完成,故对一切 n N*,都有
N*,都有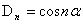 .
.
总之,数学归纳法的两个步骤,缺一不可.即都是必须的,否则将不完整,甚至导出错误的结果.
例如对于命题 .若我们放弃验证第一步,而直接证第二步,即设
.若我们放弃验证第一步,而直接证第二步,即设 时命题成立,即
时命题成立,即 ,而对于
,而对于 时,由
时,由
 (2
(2
 ,即命题对于
,即命题对于 时亦成立.能否由此得到命题正确呢?其实这个命题是错误的.但我们居然推演出了,毛病在于第一步没有验证.至于只验证第一步,而不验证第二步,这虽然只是对命题的不完全归纳,但它却无法保证命题的正确.
时亦成立.能否由此得到命题正确呢?其实这个命题是错误的.但我们居然推演出了,毛病在于第一步没有验证.至于只验证第一步,而不验证第二步,这虽然只是对命题的不完全归纳,但它却无法保证命题的正确.
3 有关代数恒等式的证明
一般采用的证明方法是在等式两边同时加上或同乘以第 项,然后适当变形可证得.
项,然后适当变形可证得.
例3 求证: ·
·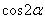 ·
· …
…

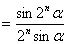 (
( ).
).
证明:(1)当 时,左边
时,左边 ,右边
,右边 ,所以当
,所以当 时,命题成立.
时,命题成立.
(2)假设当 (
( )时命题成立,即
)时命题成立,即 ·
·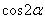 ·
· …
…

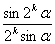 ,将此式的两边同时乘以
,将此式的两边同时乘以 ,得
,得
 ·
·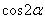 ·
· …
… ·
·

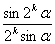 ·
·


所以当 时命题成立.综合(1)(2)可知对于任意自然数命题都成立.
时命题成立.综合(1)(2)可知对于任意自然数命题都成立.
4 有关数列命题的证明
例4:求证:等差数列前n项和的公式. ,其中
,其中 为首项,
为首项, 为公差.
为公差.
证明:(1)当 ,
, ,等式成立.
,等式成立.
(2)假设当 (
( )命题成立,即
)命题成立,即 ,那么,
,那么,


所以当 时命题成立.综合(1)(2)可知对于任意自然数命题都成立.
时命题成立.综合(1)(2)可知对于任意自然数命题都成立.
5 有关不等式的证明
⑴早期假设,合理放缩
要由“假设不等式”成立推正到“目标不等式”成立,可先尽早使用“假设不等式”,再利用辅助条件通过合理的放缩,逐步向“目标不等式”逼近.
例5证明不等式: …
…
 (n
(n )
)
证明:(1)当 时,左边
时,左边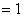 ,右边
,右边 ,左边
,左边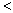 右边,不等式成立.
右边,不等式成立.
(2)假设当 (
( )不等式成立,即
)不等式成立,即 …
…
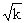
当 时,则
时,则 …
…

(现关键证明 )
)

∴ ,即当
,即当 时,不等式成立.
时,不等式成立.
综合(1)(2)可知对于任意自然数不等式都成立.
⑵等价转化,降低难度
当给出的不等式不容易直接用数学归纳法证明时,可以对命题进行等价转化,化归为证明相对容易的不等式.
例6已知数列 满足:
满足: ,
, 且
且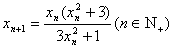 .
.
求证:数列 对于任何
对于任何 ,有
,有 成立,或对于任何
成立,或对于任何 ,有
,有
 成立.
成立.
证明:(1)当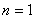 时,结论显然成立.
时,结论显然成立.
(2)假设 (
( )结论成立,即
)结论成立,即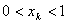 ,则
,则


∴ ,即当
,即当 时,原式成立.
时,原式成立.
由(1)(2)可知 恒成立,故
恒成立,故 时,
时, 恒成立;
恒成立;
同理 时,
时, 恒成立,即当
恒成立,即当 时,
时, 恒成立.
恒成立.
6 应用数学归纳法证明整除问题
应用数学归纳法证明整除问题,是数学归纳法的重要应用之一.这类问题涉及到整除性的知识,如果 能被
能被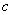 整除,那么
整除,那么 的倍数
的倍数 也能被
也能被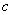 整除,如果
整除,如果 、
、 都能被
都能被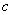 整除,那么它们的和或差
整除,那么它们的和或差 也能被
也能被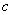 整除,从整数的基本入手,通过添项去项进行配凑,使之能够获证.
整除,从整数的基本入手,通过添项去项进行配凑,使之能够获证.
例7证明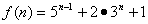 能被8整除.
能被8整除.
证明:(1)当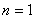 时,
时, 显然能被8整除,命题成立
显然能被8整除,命题成立
(2)假设当 时,原命题成立,即
时,原命题成立,即 能被8整除,那么,当
能被8整除,那么,当 时,
时,
 .这里的第一项由归纳假设能被8整除,第二项中
.这里的第一项由归纳假设能被8整除,第二项中 为奇数,则
为奇数,则 为偶数,故第二项4
为偶数,故第二项4 能被8整除,由整除性质可知,它们的差也能被8整除,这就是说:当
能被8整除,由整除性质可知,它们的差也能被8整除,这就是说:当 时命题也成立.即原命题对于所有自然数
时命题也成立.即原命题对于所有自然数 都成立.
都成立.
7 数学归纳法在离散数学方面的应用
离散数学以离散问题为研究对象,其中很多结论都与自然数有关,并可以用数学归纳法证明离散数学中的某些结论.如有关集合中关系及性质、树及其性质,这样既降低了证明过程的复杂性,又是推理过程更加严密清晰.
例8 已知 ,
, ,…,
,…, 是
是 个正整数,
个正整数,
 ,已知
,已知 ,证明存在结点度数分别为
,证明存在结点度数分别为 ,
, ,…,
,…, 的一棵树.
的一棵树.
证明:对结点 进行归纳证明,可构造满足条件的树
进行归纳证明,可构造满足条件的树
(1)当 时,由
时,由 ,而
,而 ,
, ,所以
,所以 ,于是存在
,于是存在 为满足条件的树.
为满足条件的树.
(2)假设当 时结论成立,即存在结点度数分别为
时结论成立,即存在结点度数分别为 ,
, ,…,
,…, 的一棵树
的一棵树 ,要证
,要证 时,结论也成立.
时,结论也成立.
由 ,
, ,…,
,…, ,
, 均为正整数,
均为正整数, 知这
知这 个数中至少有两个为一,否则
个数中至少有两个为一,否则 ,与条件矛盾.
,与条件矛盾.
不妨设 ,于是
,于是 ,
,
则

考虑 ,
, ,…,
,…, ,
,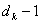 这
这 个正整数,由归纳假设知存在结点度数分别是
个正整数,由归纳假设知存在结点度数分别是 ,
, ,…,
,…, ,
,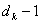 的一棵树
的一棵树 ,在
,在 中从结点度数为
中从结点度数为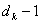 的结点
的结点 引出一条边,另一端记为
引出一条边,另一端记为 ,这样得一棵新树
,这样得一棵新树 ,在
,在 中deg
中deg ,
,
deg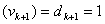 .
.
于是 ,因此,
,因此, 即为所求的一棵树.
即为所求的一棵树.
8 数学归纳法在概率论方面的应用
在概率问题中常会遇到一些与试验次数有关的重要结论,这些结论在使用数学归纳法证明时,常常需要配合使用全概率公式,从而使概率论中的数学归纳法具有自己的特色.
例9 设有 个罐子,在每个罐子里各有
个罐子,在每个罐子里各有 个白球和
个白球和 个黑球,从第一个罐子中人任取一球放到第二个罐子里,并以此类推,求从最后一个罐子里取出一个白球的概率.
个黑球,从第一个罐子中人任取一球放到第二个罐子里,并以此类推,求从最后一个罐子里取出一个白球的概率.
解析:先探索规律,设
令 “从第一个罐子里取出一个球,是白球”;
“从第一个罐子里取出一个球,是白球”; “从第二个罐子中取出一个球,是白球”.
“从第二个罐子中取出一个球,是白球”.
显然P( )
)
所求概率P( )
)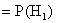 P(
P( ︳
︳ )+P(
)+P( )P(
)P( ︱
︱ )
)

 .
.
这恰与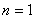 时的结论是一样的,于是可以预见,无论
时的结论是一样的,于是可以预见,无论 为什么自然数,所求的概率都应是
为什么自然数,所求的概率都应是 ,则当
,则当 时,有P(
时,有P( )
) P(
P( ︳
︳ )+P(
)+P( )P(
)P( ︱
︱ )
)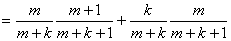
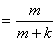 .
.
于是,结论 对所有自然数都成立.
对所有自然数都成立.
9总结
综上所述,数学归纳法在一些困难的问题中发挥着主要作用,它不仅在中学数学中有用,在我们的基础学科:数学分析高等代数等学科中也发挥着其作用.因此,数学归纳法不仅贯穿于我们数学的各门学科中,而且在我们的日常生活中也起着不同凡响的.正如华罗庚老先生在其《数学归纳法》一书中指出的那样:数学归纳法正是体现了人的认识从有限到无限的飞跃. 在人类数学的进步中起着非常广泛的作用.
3 参考文献
[1]张莉.数学归纳法的历史[J].辽宁师范大学学报(自然科学版),1999:22(2):104
[2]M克莱因,古今数学思想(第一册)[M].张理京,译.上海:上海科学技术.
[3]H伊夫斯,数学史概论(修订版)[M].欧阳绛,译.太原:山西经济出版社,1993:249.
[4]北京大学数学系.高等代数[M].北京:1988.
[5]王品超.高等数学新方法(下册)[M].中国矿业大学出版.
[7]刘世泽.数学归纳法的另外两种形式[J].数学通报
[8]Leon Henkin.On Mathematical Induction[J].American Mathematical Monthly.1960,67(4):323~328.
4 致谢
岁月如歌,光阴似箭,当再一次走在校园宁静的小路上,当再一次走进学校教学楼这座神圣的求知殿堂,看着熟悉的校园,回想一幕幕熟悉的场景,一个个熟悉的身影。此时此刻,此情此景,在这临近毕业的时节,除了深深地感谢我还能说些什么?
首先衷心地感谢我敬爱的指导老师 老师。从论文的选题、论文方案的制定、论文的开展和进行、论文结果的分析与讨论,以及论文的撰写和修改等方面,都倾注郭老师的大量心血与汗水。师从于 老师,收获是多方面的,从他渊博的知识、严谨的治学中,我体会到了知识与研究的魅力;从他认真负责的工作作风中,我学习到了勤劳与执著。在此谨向老师致以最崇高的敬意和最诚挚的感谢!
感谢长期以来一直无私关心和帮助我的挚友们。
最后,感谢在我十几年的求学生涯中始终支持我、关心我的父母和家人们。没有他们对我的支持、理解、宽容和鼓励,我不可能完成学业。他们是我前进道路上永恒的源动力!
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
新课标高二数学归纳法(经典总结)
数学归纳法极限一第一数学归纳法一般地证明一个与自然数n有关的命题Pn有如下步骤1证明当n取第一个值n0时命题成立n0对于一般数列取…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
理科数学归纳法知识总结
理科数学归纳法知识总结一基本概念1运用数学归纳法证明命题要分两步第一步是归纳奠基或递推基础第二步是归纳递推或归纳假设两步缺一不可二…
-
数学归纳法教案(新)
教材背景:归纳是一种由特殊事例导出一般规律的思维方法.归纳推理分完全归纳推理与不完全归纳推理两种.不完全归纳推理只根据一类事物中的…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…