数学归纳法
目 录
摘 要……………………………………………………………………………..1
1. 数学归纳法的定义……………………………………………………………2
1.1数学归纳法的理论依据……………..……………………………………….……2
1.2第一数学归纳法……………..……………………………………………………3
1.3第二数学归纳法………..…………………………………………………………4
2. 数学归纳法使用时易错点剖析…..……………………………………………...5
3. 数学归纳法的解题应用……………………….…………………………………6
3.1 恒等式……………………………………………………………………………6
3.2 不等式……………………………………………………………………………7
3.3 数列………………………………………………………………………………8
3.4 平面几何………………………………………………………………………..10
3.5 整数的整除性…………………………………………………………………..11
3.6 排列组合的计数………………………………………………………………..11
3.7 行列式与矩阵……………………………………………………………..……12
4.结 论………………………………………………………………………………14
参考文献………………………………………………………….………………… 14
致谢词………………………………………………………………………………15
【摘 要】数学归纳法是用来证明某些与自然数有关的数学命题的一种数学推理方法,是一种形式独特的完全归纳推理,在数学解题中有着广泛的应用。本文从数学归纳法的理论依据---皮亚诺( )的自然数的序数理论的归纳公理入手,给出数学归纳法的证明,由此得到其完整的定义,并对数学归纳法使用时易错点进行探讨,重点讨论数学归纳法在初等数学和高等数学的多种应用。
)的自然数的序数理论的归纳公理入手,给出数学归纳法的证明,由此得到其完整的定义,并对数学归纳法使用时易错点进行探讨,重点讨论数学归纳法在初等数学和高等数学的多种应用。
【关键词】 数学归纳法 证明 应用
【ABSTRACT】Mathematical induction is used to prove some natural number, related mathematical proposition of a mathematical reasoning methods, is one kind of form unique completely inductive reasoning, in mathematics problem-solving in a wide range of applications. Based on the theoretical basis of the mathematical induction -  (
( ) of the specified number theory of inductive justice given mathematical induction of proof, thus obtained the full definitions, and the mathematical induction easy wrong points discussed emphatically discussed mathematical induction in elementary mathematics and the higher mathematics the many applications.
) of the specified number theory of inductive justice given mathematical induction of proof, thus obtained the full definitions, and the mathematical induction easy wrong points discussed emphatically discussed mathematical induction in elementary mathematics and the higher mathematics the many applications.
【KEY-WORDS】Mathematical induction ; natural; Proof
数学归纳法是用来证明某些与自然数有关的数学命题的一种推理方法,它是一个递推的数学论证方法。论证的第一步是证明命题在 (或
(或 )时成立,这是递推的基础;第二步是假设在
)时成立,这是递推的基础;第二步是假设在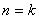 时命题成立,再证明
时命题成立,再证明 时命题也成立,这是无限递推下去的理论依据,它判断命题的正确性能否由特殊推广到一般,实际上它使命题的正确性突破了有限,达到无限。这两个步骤密切相关,缺一不可,完成了这两步,就可以断定“对任何自然数(或
时命题也成立,这是无限递推下去的理论依据,它判断命题的正确性能否由特殊推广到一般,实际上它使命题的正确性突破了有限,达到无限。这两个步骤密切相关,缺一不可,完成了这两步,就可以断定“对任何自然数(或 且
且 )结论都正确”。由这两步可以看出,数学归纳法是由递推实现归纳的,属于完全归纳。
)结论都正确”。由这两步可以看出,数学归纳法是由递推实现归纳的,属于完全归纳。
数学归纳法在数学解题中有着广泛的应用,在数学教学中常用在证明下列命题:与自然数 有关的恒等式、不等式、数列、几何、整除性、计数等等。
有关的恒等式、不等式、数列、几何、整除性、计数等等。
1. 数学归纳法的定义
数学归纳法可以分别从两个原理出发:一个是最小正整数原理,另一个就是直接从皮亚诺( )的自然数的序数理论的归纳公理。本文下面就从皮亚诺(
)的自然数的序数理论的归纳公理。本文下面就从皮亚诺( )的自然数的序数理论的归纳公理推导数学归纳法。进一步介绍第一数学归纳法和第二数学归纳法。
)的自然数的序数理论的归纳公理推导数学归纳法。进一步介绍第一数学归纳法和第二数学归纳法。
1.1 数学归纳法的理论依据
皮亚诺( )的自然数的序数理论的归纳公理:
)的自然数的序数理论的归纳公理:
设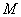
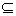
 且
且
a.  ;
;
b. 如果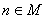
 .则
.则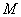 包含一切自然数,即
包含一切自然数,即
这个归纳公理就是数学归纳法证明的根据。设 是与自然数有关的的某一性质,使
是与自然数有关的的某一性质,使 成立的自然数的集合记作
成立的自然数的集合记作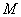 ,如果要证明性质
,如果要证明性质 对于全体自然数都成立,只要证明
对于全体自然数都成立,只要证明 ,而归纳公理就提供了证明的方法的基础,并由此派生出适应不同条件和要求的数学归纳法,常用的有第一数学归纳法与第二数学归纳法。
,而归纳公理就提供了证明的方法的基础,并由此派生出适应不同条件和要求的数学归纳法,常用的有第一数学归纳法与第二数学归纳法。
1.2 第一数学归纳法原理:
一般地,证明一个与正整数 有关的命题,采用下列步骤:
有关的命题,采用下列步骤:
第一步,验证命题 是成立的;(奠定基础步骤)
是成立的;(奠定基础步骤)
第二步,假设命题 是成立的,导出命题
是成立的,导出命题 也成立,那么这个命题对于一切正整数
也成立,那么这个命题对于一切正整数 都成立。(归纳总结步骤)
都成立。(归纳总结步骤)
证明:假设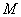 是由满足命题
是由满足命题 的自然数组成的集合,
的自然数组成的集合, ,因为
,因为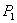 成立,
成立,
所以 .由皮亚诺的归纳公理第二步可知,
.由皮亚诺的归纳公理第二步可知,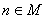
 ,根据归纳公理,
,根据归纳公理, .即
.即 对任意自然数都成立
对任意自然数都成立
这是数学归纳法最基本的形式,通常称作第一数学归纳法。其使用的步骤类似下例:
例1.用数学归纳法证明::

证明: (1)当 时,
时, ,命题显然成立
,命题显然成立
(2) 假设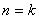 时命题成立,即
时命题成立,即
当 时
时

因为 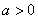 , 所以
, 所以 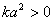
于是 
当 时命题成立
时命题成立
由(1)和(2)可知,命题对于任何自然数都成立。
1.3 第二数学归纳法原理:
对于某个与自然数 有关的命题,采用下列步骤:
有关的命题,采用下列步骤:
(1)验证命题 是成立的;(奠定基础步骤)
是成立的;(奠定基础步骤)
(2)假设命题对于正整数 时
时 成立,并在此基础上,推出
成立,并在此基础上,推出 成立。那么命题对于一切正整数
成立。那么命题对于一切正整数 来说都成立。(归纳总结步骤)
来说都成立。(归纳总结步骤)
证明:设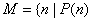 成立,
成立, ,又
,又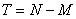 . 假设
. 假设 根据自然数的最小数原理,
根据自然数的最小数原理,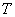 有最小数
有最小数 . 由条件第一步知,
. 由条件第一步知, ,故
,故 . 因此,1,2,…,
. 因此,1,2,…, -
- . 又根据条件第二步
. 又根据条件第二步 这和
这和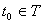 矛盾,所以
矛盾,所以 ,故
,故 ,因此,
,因此, 对于任意自然数都成立.
对于任意自然数都成立.
通常把上述数学归纳法叫做第二数学归纳法。一般使用步骤类似下面一个例题,
从上面我们得知第一数学归纳法和第二数学归纳法的理论依据是皮亚诺的自然数的序数理论的归纳公理。第一数学归纳法合第二数学归纳法用法上第一步都是验证命题 是成立,结论也相同。
是成立,结论也相同。
但是它们存在一定的差异,主要表现在第二步的归纳假设上,从两个假设可以看到第一数学归纳法是假设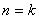 时命题成立,第二数学归纳法是假设命题对于正整数
时命题成立,第二数学归纳法是假设命题对于正整数 成立。就是讲第二数学归纳法在证明的要求上更严格,不仅要求命题在
成立。就是讲第二数学归纳法在证明的要求上更严格,不仅要求命题在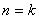 时成立,还要求列举出所有小于
时成立,还要求列举出所有小于 的自然数都成立。因为有些命题仅仅由
的自然数都成立。因为有些命题仅仅由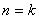 成立推出
成立推出 成立的基础不够清晰和扎实,所以才有第二数学归纳法。当然,第一数学归纳法能论证的数学命题,一定也能用第二数学归纳进行证明。
成立的基础不够清晰和扎实,所以才有第二数学归纳法。当然,第一数学归纳法能论证的数学命题,一定也能用第二数学归纳进行证明。
第二数学归纳法和第一数学归纳法一样,也是数学归纳法的一种表达形式,而且可以证明第二数学归纳法和第一数学归纳法是等价的,之所以采用不同的表达形式,旨在更便于我们对不同的要求的数学命题而使用。
2.数学归纳法使用时易错点剖析
数学归纳法是一种完全归纳推理,在应用数学归纳法时不能忽视完全归纳推理,只是做部分归纳,从而得出错误的结论。如法国数学家费马曾考查了
 ,
, ,
, ,
,
而5,17,257,65537都为素数,于是,他就断言:对于自然数 ,
, 都为素数。但是,他的猜想是错误的。瑞士数学家欧拉发现,当
都为素数。但是,他的猜想是错误的。瑞士数学家欧拉发现,当 时
时
 +1=4294967297=641×6700417就是一个合数,这就说明不完全归纳法存在严重的缺陷。
+1=4294967297=641×6700417就是一个合数,这就说明不完全归纳法存在严重的缺陷。
在数学归纳法使用证明过程中的两步都是必不可少,否则,就会在没有验证第一步的情况下,而得出错误的结论的问题。例如:
数学归纳法证明:2+4+6+…+2 =
=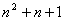
假设当 时,等式成立,
时,等式成立,
当 时, 2+4+6+…+2
时, 2+4+6+…+2 +
+ =
= ,验证等式也成立.从而得出对任何自然数,等式成立的结论,但是 当
,验证等式也成立.从而得出对任何自然数,等式成立的结论,但是 当 时,左边等于2,右边等于3,命题不成立.
时,左边等于2,右边等于3,命题不成立.
在数学归纳法使用过程中更多出错的在于第二步骤。一个常见的错误是:在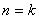 时命题成立的假设下,形式上得出
时命题成立的假设下,形式上得出 成立结论,并没有在前个假设的基础上进行有效地实质上的推导,而仅仅是形式上的推导。
成立结论,并没有在前个假设的基础上进行有效地实质上的推导,而仅仅是形式上的推导。
例如,设  (
( =1,2,…,
=1,2,…, ),且
),且 +…+
+…+ =1 证明:
=1 证明:

当 时
时  ,
, 命题成立
命题成立
假设当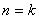 时,等式成立,即
时,等式成立,即
当 时,
时, 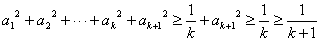 命题成立.
命题成立.
但应注意 和
和 时的前提条件分别为:
时的前提条件分别为: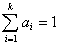 和
和 
既然当 时的前提条件变化了,就不能直接套用
时的前提条件变化了,就不能直接套用 的结论,而应设法改造前提条件,使之符合归纳假设的要求。
的结论,而应设法改造前提条件,使之符合归纳假设的要求。
3.数学归纳法的解题应用
数学归纳法在数学解题中有着广泛的应用,可以证明与自然数有关的命题。本文选取数学教学中几类命题使用数学归纳法证明:与自然数n有关的恒等式、不等式、数列、几何、整除性、计数及行列式与矩阵,加深对数学归纳法的认识。
3.1 恒等式
在涉及到与自然数有关的恒等式中多数都可以用数学归纳法证明,在初等数学教学中的许多代数式,三角式的恒等变换的命题用数学归纳法可以有效地证明。在证明过程中要注意式子的恒等变换和法则的正确使用。下面就举三角式的恒等证明来说明:
例3.用数学归纳法证明:对于正整数 ,
,
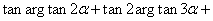 …
… =
=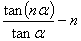
分析:本题第一步的验证要取 ,在第二步的证明中应在归纳假设的基础上正确地使用正切的和角公式
,在第二步的证明中应在归纳假设的基础上正确地使用正切的和角公式
证明: (1)当 时,右边=
时,右边= =
= =
=
= =左边,等式成立
=左边,等式成立
(2)假设当 时,等式成立,就是
时,等式成立,就是
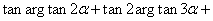 …
… =
=
则当n=k+1时, 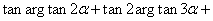
…
+
=
 =
=
本题在第(2)步的证明过程中使用了正切和差角的变形形式,即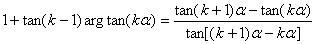
在用数学归纳法证明三角命题时,应针对 时命题的特征,合理地选择和使用三角公式。证明三角恒等式时,常动用有关三角知识、三角公式及三角的变换法。
时命题的特征,合理地选择和使用三角公式。证明三角恒等式时,常动用有关三角知识、三角公式及三角的变换法。
3.2 不等式
在上面我们看到数学归纳法在等式的应用,那么在不等式中数学归纳法是怎么样的呢?以下用例题说明:
例4: 设 >0(
>0( =1,2,…,n),且
=1,2,…,n),且
+…+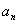 =1。证明:
=1。证明:

证明:(1)当 时,因
时,因 ,故
,故
又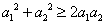 ,所以
,所以



(2)假设当 时命题成立,即在
时命题成立,即在 +…+
+…+ =1且a>0(
=1且a>0( =1,2, …,k)的条件下有
=1,2, …,k)的条件下有

+…+

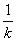
则当 时,因为
时,因为
 +…+
+…+ +
+ =1,且各
=1,且各 >0
>0
根据 +…+
+…+ +
+ =1,且各
=1,且各 >0,0<
>0,0< <1,故1-
<1,故1- >0因而满足归纳假设
>0因而满足归纳假设 +…+
+…+

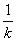 所应满足的条件,
所应满足的条件,
所以 
+…+

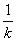
 +…+
+…+


 +…+
+…+ +
+

 +
+
因为 
+ -
- =
=
=
所以  +…+
+…+ +
+

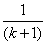
因此,原命题对大于1的自然数都成立.
用数学归纳法证明不等式,宜先比较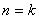 与
与 这两个不等式间的差异,以决定
这两个不等式间的差异,以决定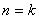 时不等式做何种变形,一般地只能变出
时不等式做何种变形,一般地只能变出 等式的一边,然后再利用比较、分析、综合、放缩及不等式的传递性来完成由
等式的一边,然后再利用比较、分析、综合、放缩及不等式的传递性来完成由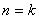 成立推出
成立推出 不等式成立的证明.
不等式成立的证明.
3.3 数列
数列在数学教学和实际生活中有着广泛的应用,它与函数、方程、不等式、三角、复数、立体几何和解析几何都有着密切的关系,涉及数列的应用性问题也屡见不鲜,以下例题仅从数学归纳法去解题。
例5: 设数列{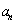 }的前
}的前 项和为
项和为 ,若对于所有的自然数
,若对于所有的自然数 ,都有
,都有 =
= ,证明{
,证明{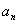 }是等差数列。
}是等差数列。
分析:要证明{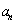 }是等差数列,可以证明其通项符合等差数列的通项公式的形式,即证:
}是等差数列,可以证明其通项符合等差数列的通项公式的形式,即证: =
= +(
+( -1)
-1) 。命题与
。命题与 有关,考虑是否可以用数学归纳法进行证明。
有关,考虑是否可以用数学归纳法进行证明。
证明: 设 -
- =
= ,猜测
,猜测  =
= +(
+( -1)
-1)
当 =1时,
=1时,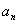 =
= , 所以 当
, 所以 当 =1时猜测正确
=1时猜测正确
当 =2时,
=2时,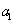
 +(2-1)
+(2-1)  =
=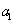 +
+ =
=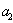 , 所以 当
, 所以 当 =2时猜测正确
=2时猜测正确
假设当 =
= (
( ≥2)时,猜测正确,即:
≥2)时,猜测正确,即: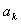 =
= +(
+( -1)
-1)
当 =
= +1时,
+1时, =S
=S -S
-S =
= -
-
将 =
= +(
+( -1)
-1)  代入上式, 得到
代入上式, 得到
2 =(k+1)(
=(k+1)( 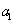 +
+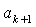 )-2
)-2
 -
- (
( -1)
-1)
整理得 ( -1)
-1)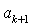 =(
=( -1)
-1)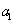 +
+ (
( -1)
-1)
因为 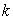 ≥2, 所以
≥2, 所以 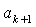 =
= +
+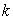
 ,即
,即 =
= +1时猜测正确
+1时猜测正确
综上所述,对所有的自然数 ,都有
,都有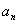 =
= +(
+( -1)
-1) ,从而{
,从而{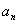 }是等差数列。
}是等差数列。
将证明等差数列的问题转化成证明数学恒等式关于自然数n成立的问题。在证明过程中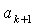 的得出是本题解答的关键,利用了已知的等式
的得出是本题解答的关键,利用了已知的等式 =
=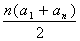 、数列中通项与前
、数列中通项与前 项和的关系
项和的关系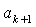 =
=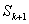 -
- 建立含
建立含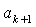 的方程,代入假设成立的式子
的方程,代入假设成立的式子 =
= +(
+( -1)
-1) 解出来
解出来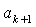 。另外本题注意的一点是不能忽视验证
。另外本题注意的一点是不能忽视验证 =1、
=1、 =2的正确性,用数学归纳法证明时递推的基础是
=2的正确性,用数学归纳法证明时递推的基础是 =2时等式成立, 因为, 由(
=2时等式成立, 因为, 由( -1)
-1)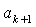 =(
=( -1)
-1) +
+ (
( -1)
-1) 得到
得到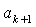 =
= +
+
 的
的 ≥2.
≥2.
3.4 平面几何
数学归纳法的应用在几何里也有着独特的应用,关键要分析增加一条曲线或直线后,点、线段、曲线段、平面块在 基础上净增多少,于是就找出了相应的递推关系
基础上净增多少,于是就找出了相应的递推关系
 ,下面让我们来看两个例题。
,下面让我们来看两个例题。
例6:平面上 条直线 把平面分成若干个区域。证明,用两种颜色给这些区域染色,使任意两个相邻的区域(即有公共边界的区域)所染颜色不同。
条直线 把平面分成若干个区域。证明,用两种颜色给这些区域染色,使任意两个相邻的区域(即有公共边界的区域)所染颜色不同。
证明:对直线的条数 归纳。
归纳。
(1) 当 时,平面分成两个半平面,显然命题成立.
时,平面分成两个半平面,显然命题成立.
(2) 设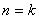 时命题成立,对于
时命题成立,对于 条直线
条直线 …
…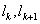 ,先将
,先将 去掉,由归纳假设可知,被
去掉,由归纳假设可知,被 …
…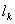 分割成的区域可以用两种颜色正确染色(即按踢给条件),再将
分割成的区域可以用两种颜色正确染色(即按踢给条件),再将 添进去,这时一些区域被
添进去,这时一些区域被 分成两个区域。将位于 某一侧的半平面内的所有区域改染相反的颜色,另一个半平面内的区域染色不变,这样我们仍然得到正确的染色。这说明
分成两个区域。将位于 某一侧的半平面内的所有区域改染相反的颜色,另一个半平面内的区域染色不变,这样我们仍然得到正确的染色。这说明 =
= +1时,命题成立
+1时,命题成立
由(1)、(2)可知,对所有的 ,命题成立
,命题成立
例7.证明,当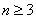 时,
时, 边形的内角和等于
边形的内角和等于
 .
.
对于这个命题 来说是没有任何意义.因此我们从
来说是没有任何意义.因此我们从 开始用数学归纳法证明.
开始用数学归纳法证明.
 (1)当
(1)当 时,命题成立,因为三角形的内角和等于
时,命题成立,因为三角形的内角和等于 =(3-2)
=(3-2) .
.
(2)假设 时命题成立.我们看任意一个
时命题成立.我们看任意一个 边形
边形
 (图1).连结
(图1).连结
 ,那么
,那么
 的内角和等于三角形
的内角和等于三角形

 的内角和再加上
的内角和再加上 边形
边形

 的内角和.前者等于
的内角和.前者等于 ,后者由学归纳法假定,等于
,后者由学归纳法假定,等于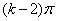 .因此
.因此 边形
边形
 的内和等于
的内和等于 +
+ =
=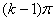 =
=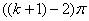 .命题得证. 图1
.命题得证. 图1
运用数学归纳法证明几何问题,一般从特殊到一般的探索、归纳、猜想及证明的思维方式进行求解,证题的关键是弄清增加一条直线能够增加多少不同的交点,增加的交点会导致几何那些方面的的改变。解此类问题常运用几何图形的性质,可注意加以运用。 
3.5 整数的整除性
设 均为整数,如果存在一个整数
均为整数,如果存在一个整数 ,使得
,使得 ,则称
,则称 整除
整除 ,通常记为
,通常记为 ,由于整除性问题本身是在整除的范围内考虑的,所以处理整除性问题时可以尝试用数学归纳法来解决
,由于整除性问题本身是在整除的范围内考虑的,所以处理整除性问题时可以尝试用数学归纳法来解决
例8. 设 ,证明:
,证明:
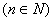
证明:(1) 当 时,
时, ,命题成立;
,命题成立;
(2) 设 时命题成立,即
时命题成立,即 ,于是
,于是

因为 
所以 

由(1)、(2)知对所有的 ,命题成立.
,命题成立.
用数学归纳法证明整除问题时,首先要从要证的式子中拼凑出假设成立的式子,然后证明剩余的式子也能被某式(数)整除,这是数学归纳法证明整数的整除性问题的一个技巧。
3.6 排列组合计数
求出一个有限集 中元素的个数(记为|
中元素的个数(记为| |)称为计数。排列组合问题就属于计数问题之列。在这一列问题中,数学归纳法也得到广泛的应用。
|)称为计数。排列组合问题就属于计数问题之列。在这一列问题中,数学归纳法也得到广泛的应用。
例9. 设有2 张卡片,上面分别写着1,2, …,
张卡片,上面分别写着1,2, …, 这
这 个数。现在从中任意取出两张,设其号码为
个数。现在从中任意取出两张,设其号码为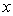 和
和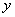 ,且
,且 。设满足
。设满足 的取法
的取法 共
共 种,证明:
种,证明: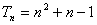
证明:(1)当 时,共2张卡片,
时,共2张卡片, ,所以
,所以 ,命题成立;
,命题成立;
(2)设 . 当
. 当 ,从
,从 张卡片:1,2, …,
张卡片:1,2, …, ,
, ,
, 中任取两张,两张中包含
中任取两张,两张中包含 的取法为
的取法为 ,
, ,…,
,…,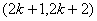 ,显然,
,显然, 种取法均满足
种取法均满足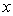 +
+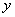

 。在其余的取法中,依归纳假设共有
。在其余的取法中,依归纳假设共有 =
= +k-1种,满足
+k-1种,满足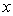 +
+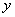
 2k,其中满足
2k,其中满足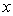 +
+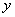 =
= 的为
的为
(1, 2 -1),(2, 2
-1),(2, 2 -2),…,(
-2),…,( -1,
-1,  +1),共
+1),共 -1种,满足
-1种,满足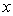 +
+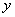 =2
=2 +1的为(1, 2
+1的为(1, 2 ),(2, 2
),(2, 2 -1),…,(
-1),…,( ,
,  +1),共
+1),共 种。
种。
综上所述可得
 =[
=[ +
+ -1-(
-1-( -1)-
-1)- ]+(2
]+(2 +1)+2
+1)+2 =
= 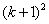 +(
+( +1)-1
+1)-1
由(1)、(2)可知,对所有的 ,命题成立.
,命题成立.
排列组合计数知识、方法、技能组合计数就是计算集合的元素个数。它是组合数学的重要组成部分 . 在具体问题中给出的集合各式各样,都具有实际意义,而且集体中的元素是由某些条件所确定的,要判定一个元素是否属于某集合 ,已非易事,要确定
,已非易事,要确定 的元素个数就更难了 . 这正是研究计算问题的原因。解决组合计算问题虽然不需要高深理论知识,却需要重要的计算原理与思想方法,数学归纳法就是一种。
的元素个数就更难了 . 这正是研究计算问题的原因。解决组合计算问题虽然不需要高深理论知识,却需要重要的计算原理与思想方法,数学归纳法就是一种。
3.7 行列式与矩阵
行列式与矩阵的计算灵活多变,需要有较强的技巧。当然,任何一个n 阶行列式都可以由它的定义去计算其值。但由定义可知, 阶行列式的展开式有
阶行列式的展开式有 !项,计算量很大,一般情况下不用此法。如果选择好的方法,从而达到化繁为简的功效。
!项,计算量很大,一般情况下不用此法。如果选择好的方法,从而达到化繁为简的功效。
例10. 证明范得蒙 行列式:
行列式:
 其中
其中 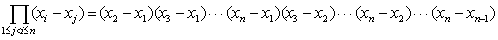
证明 :(1)当 时,
时, ,等式成立
,等式成立
(2)假设等式对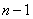 阶范得蒙行列式成立,即
阶范得蒙行列式成立,即
对n 阶范得蒙行列式:

按第一列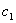 展开并提取公因子,得
展开并提取公因子,得

后面的行列式是一个 阶范得蒙行列式
阶范得蒙行列式 ,
,
由归纳假设可写作 ,代入上式便得
,代入上式便得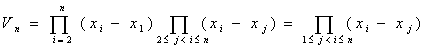 .
.
由(1)、(2)可知,对所有的 ,命题成立.
,命题成立.
例11. 求证:

证明 :(1)当 时,结论显然成立
时,结论显然成立
(2)假设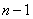 命题成立,即
命题成立,即

当取 时
时

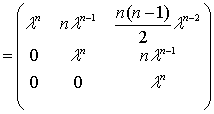
由(1)、(2)可知,对所有的 ,命题成立.
,命题成立.
在解决行列式与矩阵问题时,选择一种好的方法不仅能达到事半功倍的效果,更能体现学习高等数学的功底。计算行列式与矩阵的方法比较灵活,同一行列式与矩阵可以有多种计算方法;有的行列式计算需要几种方法综合应用.在计算时,首先要仔细考察行列式在构造上的特点,再考察它是否能用常用的几种方法,如果行列式与矩阵中有与自然数 有关,我们可考虑用数学归纳法去证明,再利用它们的性质对它进行变换,然后求解。
有关,我们可考虑用数学归纳法去证明,再利用它们的性质对它进行变换,然后求解。
4. 结 论
数学归纳法主要是针对一些自然数 的相关命题,所以在证明和自然数
的相关命题,所以在证明和自然数 有关的式子中有着不可替代的作用,对于一些和自然数
有关的式子中有着不可替代的作用,对于一些和自然数 有关的长式子、繁式子都有化长为短、化繁为简的功效。用数学归纳法证明数学问题时,要注意它的两个步骤缺一不可,第一步是命题递推的基础,第二步是命题递推的依据,也是证明的关键和难点,两个步骤各司其职,互相配合,同时,数学归纳法的证明步骤与格式的规范是数学归纳法的特征,如
有关的长式子、繁式子都有化长为短、化繁为简的功效。用数学归纳法证明数学问题时,要注意它的两个步骤缺一不可,第一步是命题递推的基础,第二步是命题递推的依据,也是证明的关键和难点,两个步骤各司其职,互相配合,同时,数学归纳法的证明步骤与格式的规范是数学归纳法的特征,如 时的假设是第二步证明的“已知”步证明时一定要用到它,否则就不是数学归纳法。从上面不难看出,在数学中,数学归纳法是一种相当成熟的数学证明方法,因此它的应用也是极其广泛的,它有着其他方法不可取代的地位。
时的假设是第二步证明的“已知”步证明时一定要用到它,否则就不是数学归纳法。从上面不难看出,在数学中,数学归纳法是一种相当成熟的数学证明方法,因此它的应用也是极其广泛的,它有着其他方法不可取代的地位。
参考文献
[1] 蒋文蔚,杨廷龄.数学归纳法[M]. 北京:北京师范大学出版社,1985
[2] 张明志, 数学归纳法[J].四川:四川教育出版社,1985
[3] 张禾瑞,郝鈵新 ,高等代数[M].第五版,北京:高等教育出版社.2007.6
[4] 李长明,周焕山.初等数学研究[M]. 北京:高等教育出版社.1995
致 谢 词
感谢我的指导老师xxx,对我论文的构思和悉心指导。他严肃的科学态度,严谨的治学精神,精益求精的工作作风,深深地感染和激励着我。两年多来,数学教研室的课任老师不仅在学业上给我以精心指导,同时还在思想、生活上影响着我,在此谨向全体课任老师致以诚挚的谢意和崇高的敬意。
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
新课标高二数学归纳法(经典总结)
数学归纳法极限一第一数学归纳法一般地证明一个与自然数n有关的命题Pn有如下步骤1证明当n取第一个值n0时命题成立n0对于一般数列取…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
理科数学归纳法知识总结
理科数学归纳法知识总结一基本概念1运用数学归纳法证明命题要分两步第一步是归纳奠基或递推基础第二步是归纳递推或归纳假设两步缺一不可二…
-
数学归纳法教案(新)
教材背景:归纳是一种由特殊事例导出一般规律的思维方法.归纳推理分完全归纳推理与不完全归纳推理两种.不完全归纳推理只根据一类事物中的…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…