用数学归纳法证明数列不等式
【例1】(20##全国大纲卷理22)函数 ,定义数列
,定义数列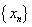 如下:
如下: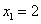 ,
,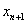 是过两点
是过两点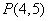 、
、 的直线
的直线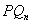 与
与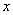 轴交点的横坐标.
轴交点的横坐标.
(1)证明: ;
;
(2)求数列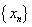 的通项公式.
的通项公式.
【证】(1)证:直线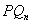 的方程为
的方程为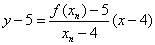 ,即
,即 ,
,
令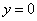 ,解得
,解得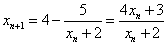 .
.
下用数学归纳法证明 :
:
① 当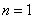 时,
时,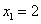 ,所以
,所以 .
.
② 假设当 时结论成立,即
时结论成立,即 ,则当
,则当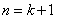 时,
时,
由 ,得
,得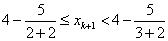 ,即
,即 ,故
,故 .
.
由①②知,对一切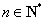 都有
都有 .
.
从而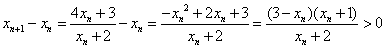 ,故
,故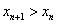 .
.
综上, .
.
(2)解:由(1)知,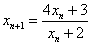 ,则
,则 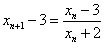 ①,
①,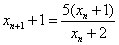 ②,
②,
①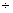 ②,得
②,得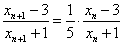 ,故数列
,故数列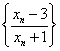 是首项为
是首项为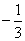 ,公比为
,公比为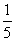 的等比数列.
的等比数列.
因此,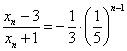 ,解得:
,解得: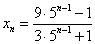
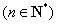 .
.
【例2】已知函数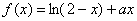 在开区间(0,1)内是增函数.
在开区间(0,1)内是增函数.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若数列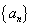 满
满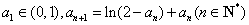 ,证明:
,证明: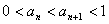 .
.
(Ⅰ)解: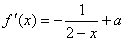 ,由于f (x)在(0,1)内是增函数,
,由于f (x)在(0,1)内是增函数,
∴ 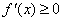 ,即
,即 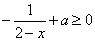 在x∈(0,1)时恒成立.
在x∈(0,1)时恒成立.
∴  恒成立,
恒成立,
而 -2<x-2<-1,
∴ 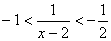 ,
,
即 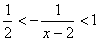 ,
,
∴ 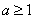 即为所求.
即为所求.
(Ⅱ) 证明:① 当n=1时,由题设知a1∈(0,1).
② 假设当n=k时,不等式成立,即ak∈(0,1),则
当n=k+1时,由(Ⅰ)知,f(x)=ln(2-x)+x在(0,1)上是增函数
∴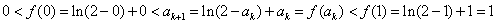 ,
,
即ak+1∈(0,1),故n=k+1时命题成立.
根据① ② 知0<an<1,n∈N*.
又 ∵  ,
,
∴ 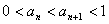 .
.
【例3】已知函数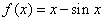 ,数列{
,数列{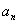 }满足:
}满足: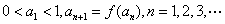 ,证明:
,证明:
(Ⅰ) 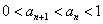 ;(Ⅱ)
;(Ⅱ) 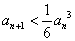 .
.
证明:(Ⅰ) 先用数学归纳法证明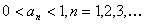
① 当n=1时,由已知,结论成立.
② 假设当n=k时结论成立,即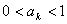 ,
,
因为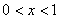 时,
时,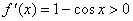 ,
,
所以 在(0,1)上是增函数,又
在(0,1)上是增函数,又 在[0,1]上连续,
在[0,1]上连续,
从而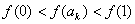 ,即
,即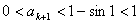 ,
,
故当n=k+1时,结论成立.
由①②可知,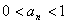 对一切正整数都成立.
对一切正整数都成立.
又因为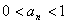 时,
时,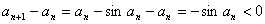 ,
,
所以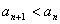 ,综上所述
,综上所述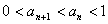 .
.
(Ⅱ) 设函数 ,
,
由(Ⅰ)可知,当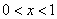 时,
时,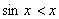 .
.
从而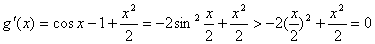 ,
,
所以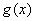 在(0,1)上是增函数.
在(0,1)上是增函数.
又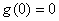 ,
,
所以当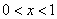 时,
时,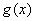 >0成立.
>0成立.
于是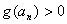 ,即
,即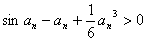 ,
,
故 .
.
【例4】已知函数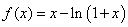 ,数列
,数列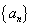 满足
满足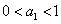 ,
,  ; 数列
; 数列 满足
满足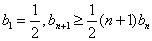 ,
, 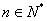 .求证:
.求证:
(Ⅰ)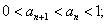
(Ⅱ)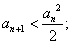
(Ⅲ)若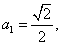 则当n≥2时,
则当n≥2时,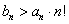 .(
.( 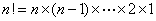 )
)
解: (Ⅰ)先用数学归纳法证明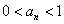 ,
,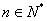 .
.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即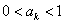 .则当n=k+1时,因为0<x<1时,
.则当n=k+1时,因为0<x<1时,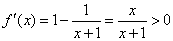 ,所以f(x)在(0,1)上是增函数.
,所以f(x)在(0,1)上是增函数.
又f(x)在 上连续,所以f(0)<f(
上连续,所以f(0)<f(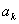 )<f(1),即0<
)<f(1),即0<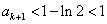 .
.
故当n=k+1时,结论也成立. 即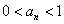 对于一切正整数都成立.
对于一切正整数都成立.
又由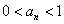 , 得
, 得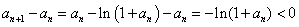 ,从而
,从而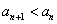 .
.
综上可知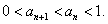
(Ⅱ)构造函数g(x)= -f(x)=
-f(x)= 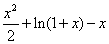 , 0<x<1,
, 0<x<1,
由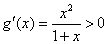 ,知g(x)在(0,1)上增函数.又g(x)在
,知g(x)在(0,1)上增函数.又g(x)在 上连续,所以g(x)>g(0)=0.
上连续,所以g(x)>g(0)=0.
因为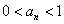 ,所以
,所以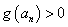 ,即
,即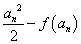 >0,从而
>0,从而
(Ⅲ) 因为 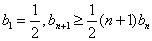 ,所以
,所以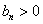 ,
,
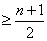 ,
,
所以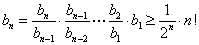 ————①
————①
由(Ⅱ)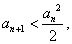 知:
知: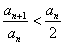 , 所以
, 所以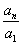 =
=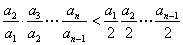 ,
,
因为 , n≥2,
, n≥2, 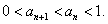
所以 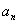
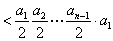 <
< <
< =
=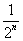 ————② .
————② .
由①② 两式可知: 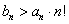 .
.
【例5】 设函数 与数列
与数列 满足以下关系:
满足以下关系:
① 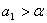 ,其中
,其中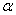 是方程
是方程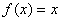 的实根;
的实根;
② 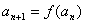 ;
;
③  的导数
的导数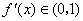 .
.
(Ⅰ) 求证: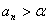 ;
;
(Ⅱ) 判断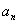 与
与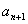 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(Ⅰ) 证:① 当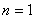 时,
时,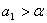 ,不等式成立.
,不等式成立.
② 假设当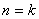 时不等式成立,即
时不等式成立,即 ,则
,则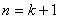 时,
时,
∵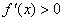 ,则
,则 递增.
递增.
∴ ,即
,即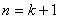 时不等式也成立.
时不等式也成立.
由①、②知,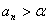 对一切
对一切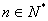 都成立.
都成立.
(Ⅱ) 解: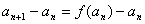 ,
,
设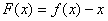 ,则
,则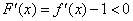 ,
,
∴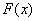 递减,而
递减,而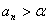 ,
,
∴ ,
,
即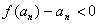 ,亦即
,亦即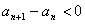 ,
,
∴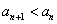 .
.
【例6】(2005江西)已知数列
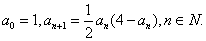
(1)证明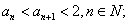
(2)求数列 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,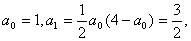 ∴
∴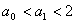 ,命题正确.
,命题正确.
2°假设n=k时有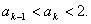
则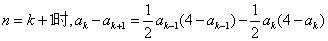
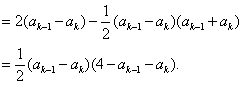
而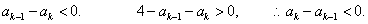
又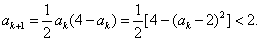
∴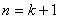 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有
方法二:用数学归纳法证明:
1°当n=1时,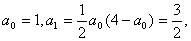 ∴
∴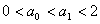 ;
;
2°假设n=k时有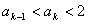 成立,
成立,
令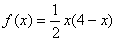 ,
, 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: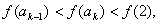 即
即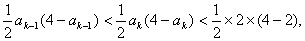
也即当n=k+1时  成立,
成立,
所以由1°、2°知,对一切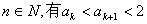
(2)下面来求数列的通项: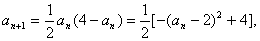 所以
所以
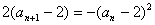
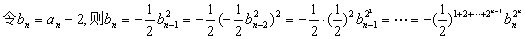 ,
,
又bn=-1,所以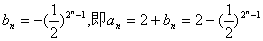
【拓展题】
【例】、数列 满足
满足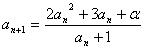 ,且
,且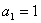 .(1)当
.(1)当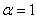 时,求数列
时,求数列 的通项公式;
的通项公式;
(2)若不等式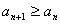 对一切
对一切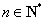 恒成立,求
恒成立,求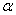 的取值范围;
的取值范围;
(3)当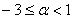 时,证明:
时,证明: .
.
解:(1)当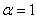 时,
时, .
.
(2)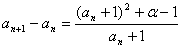 ①,要使
①,要使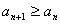 对一切
对一切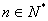 恒成立,
恒成立,
至少需使 成立
成立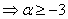 .
.
下面先用数归法证明:当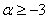 时,
时,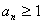 (略),再由①知
(略),再由①知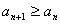 恒成立.
恒成立.
所以 为所求.
为所求.
(3)当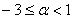 时,由(2)知
时,由(2)知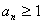 ,则由
,则由
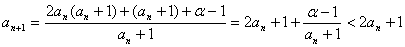
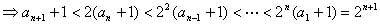
 ,
,
从而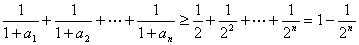 ,等号当且仅当
,等号当且仅当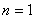 时成立.
时成立.
(2009安徽理21)首项为正数的数列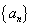 满足
满足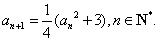 (1)证明:若
(1)证明:若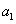 为奇数,
为奇数,
则对一切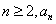 都是奇数;(2)若对一切
都是奇数;(2)若对一切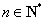 都有
都有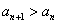 ,求
,求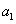 的取值范围.
的取值范围.
略解:(1)已知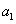 是奇数,假设
是奇数,假设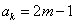 是奇数,其中
是奇数,其中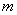 为正整数,
为正整数,
则由递推关系得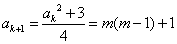 是奇数.(因为
是奇数.(因为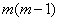 是偶数)
是偶数)
根据数学归纳法,对任何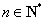 ,
,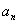 都是奇数.
都是奇数.
(2)(方法一)由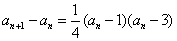 知,
知,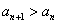 当且仅当
当且仅当 或
或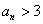 .
.
另一方面,若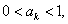 则
则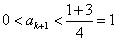 ;若
;若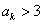 ,则
,则
根据数学归纳法,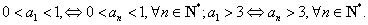
综合所述,对一切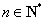 都有
都有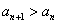 的充要条件是
的充要条件是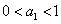 或
或 .
.
(方法二)由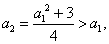 得
得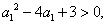 于是
于是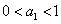 或
或 .
.
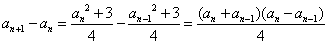 ,因为
,因为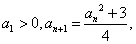
所以所有的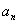 均大于
均大于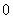 ,因此
,因此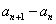 与
与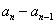 同号.
同号.
根据数学归纳法,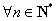 ,
,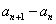 与
与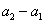 同号.
同号.
因此,对一切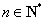 都有
都有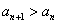 的充要条件是
的充要条件是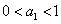 或
或 .
.
第二篇:数学归纳法证明不等式2







-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
新课标高二数学归纳法(经典总结)
数学归纳法极限一第一数学归纳法一般地证明一个与自然数n有关的命题Pn有如下步骤1证明当n取第一个值n0时命题成立n0对于一般数列取…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
理科数学归纳法知识总结
理科数学归纳法知识总结一基本概念1运用数学归纳法证明命题要分两步第一步是归纳奠基或递推基础第二步是归纳递推或归纳假设两步缺一不可二…
-
数学归纳法教案(新)
教材背景:归纳是一种由特殊事例导出一般规律的思维方法.归纳推理分完全归纳推理与不完全归纳推理两种.不完全归纳推理只根据一类事物中的…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
数学归纳法的分析探讨
数学归纳法的分析探讨谢立亚,兰州大学附属中学(甘肃兰州730000)数学归纳法是数学中的一个重要的证明方法,也是中学数学的一个重要…
-
高考数学重点难点31数学归纳法总结
重点难点31数学归纳法解题数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊…
-
数学归纳法应用总结
数学归纳法的应用数学归纳法是高考考查的重点内容之一.类比与猜想是应用数学归纳法所体现的比较突出的思想,抽象与概括,从特殊到一般是应…
-
《数学归纳法及其应用举例》网络在教学中的应用,数学参赛教案设计者:赣榆县厉庄韩冬
《数学归纳法及其应用举例》教案学校:连云港市赣榆县厉庄镇中心小学姓名:韩冬教学目标:1.认知目标:了解数学归纳法的原理,掌握用数学…